《2025年海淀单元测试AB卷七年级数学下册沪科版》

1. 若分式$\frac{x^{2}-36}{x + 6}$的值等于0，则$x$的值为( )
A. $\pm6$
B. 0
C. -6
D. 6

答案： D

2. 下列分式中，是最简分式的是( )
A. $\frac{x^{2}-1}{x^{2}+1}$
B. $\frac{x + 1}{x^{2}-1}$
C. $\frac{x^{2}-36}{2x + 12}$
D. $\frac{x^{2}-2xy + y^{2}}{x^{2}-xy}$

答案： A

3. 计算$(1+\frac{1}{x})\div\frac{x^{2}+2x + 1}{x}$的结果是( )
A. $x + 1$
B. $\frac{1}{x + 1}$
C. $\frac{x}{x + 1}$
D. $\frac{x + 1}{x}$

答案： B

4. 若$(\frac{4}{a^{2}-4}+\frac{1}{2 - a})\cdot w = 1$，则$w =$( )
A. $a + 2$
B. $-a + 2$
C. $a - 2$
D. $-a - 2$

答案： D

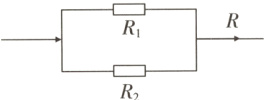
5. 新教材 变式题 电视机、摄像机等电器的电路中有许多的元件，它们都具有电阻. 如图所示，当两个电阻$R_{1},R_{2}$并联时，总电阻满足$\frac{1}{R}=\frac{1}{R_{1}}+\frac{1}{R_{2}}$，若$R_{1}=2R_{2},R = 10\ \Omega$，则$R_{1},R_{2}$的值分别为( )

A. $30\ \Omega,15\ \Omega$
B. $\frac{20}{3}\ \Omega,\frac{10}{3}\ \Omega$
C. $15\ \Omega,30\ \Omega$
D. $\frac{10}{3}\ \Omega,\frac{20}{3}\ \Omega$

答案： A [解析]设$R_{2}=x$，则$R_{1}=2R_{2}=2x$.$\because\frac{1}{R}=\frac{1}{R_{1}}+\frac{1}{R_{2}}$，$R = 10\Omega$，$\therefore\frac{1}{10}=\frac{1}{2x}+\frac{1}{x}$，解得$x = 15$，经检验，$x = 15$是原方程的解，$\therefore R_{1}=30\Omega$，$R_{2}=15\Omega$.故选A.

6. 辨思维 一题多解 已知$n＞1,M=\frac{n}{n - 1},N=\frac{n - 1}{n},P=\frac{n}{n + 1}$，则$M,N,P$的大小关系为( )
A. $M＞N＞P$
B. $M＞P＞N$
C. $P＞M＞N$
D. $P＞N＞M$

答案： B [解析]$\because n＞1$，$M=\frac{n}{n - 1}$，$N=\frac{n - 1}{n}$，$P=\frac{n}{n + 1}$，$\therefore M - P=\frac{n}{n - 1}-\frac{n}{n + 1}=\frac{n^{2}+n - n^{2}+n}{n^{2}-1}=\frac{2n}{(n + 1)(n - 1)}＞0$，$P - N=\frac{n}{n + 1}-\frac{n - 1}{n}=\frac{n^{2}-n^{2}+1}{n(n + 1)}=\frac{1}{n(n + 1)}＞0$，则$M＞P＞N$.

7. 已知$x^{2}-2x - 1 = 0$，则$x^{2}+\frac{1}{x^{2}}$的值为( )
A. 1
B. 2
C. 4
D. 6

答案： D [解析]$\because x^{2}-2x - 1 =0$，易得$x\neq0$，$\therefore$两边同除以$x$，得$x - 2 - \frac{1}{x}=0$，$\therefore(x - \frac{1}{x})^{2}=4$，即$x^{2}+\frac{1}{x^{2}}-2 =4$，$\therefore x^{2}+\frac{1}{x^{2}}=6$.故选D.