第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
1.(常德中考)在$\frac{33}{17},\sqrt{3},-\sqrt[3]{8},\pi,2025$这五个数中,无理数的个数为( )
A.2
B.3
C.4
D.5
A.2
B.3
C.4
D.5
答案:
A
2.(合肥期中)下列各式计算正确的是( )
A.$\sqrt{36}=\pm6$
B.$\pm\sqrt[3]{\frac{27}{8}}=\pm\frac{3}{2}$
C.$\sqrt{(-5)^{2}}=-5$
D.$\sqrt{-100}=10$
A.$\sqrt{36}=\pm6$
B.$\pm\sqrt[3]{\frac{27}{8}}=\pm\frac{3}{2}$
C.$\sqrt{(-5)^{2}}=-5$
D.$\sqrt{-100}=10$
答案:
B
3.(绍兴中考)下列计算正确的是( )
A.$(a^{2}+ab)\div a=a + b$
B.$a^{2}\cdot a=a^{2}$
C.$(a + b)^{2}=a^{2}+b^{2}$
D.$(a^{3})^{2}=a^{5}$
A.$(a^{2}+ab)\div a=a + b$
B.$a^{2}\cdot a=a^{2}$
C.$(a + b)^{2}=a^{2}+b^{2}$
D.$(a^{3})^{2}=a^{5}$
答案:
A
4. 不等式组$\begin{cases}x<3 \\ x\geqslant1\end{cases}$的解集在数轴上表示为( )


答案:
C
5.(滨州中考)若$8x^{m}y$与$6x^{3}y^{n}$的和是单项式,则$(m + n)^{3}$的平方根为( )
A.4
B.8
C.$\pm4$
D.$\pm8$
A.4
B.8
C.$\pm4$
D.$\pm8$
答案:
D
6.(株洲中考)下列各选项中因式分解正确的是( )
A.$x^{2}-1=(x - 1)^{2}$
B.$a^{3}-2a^{2}+a=a^{2}(a - 2)$
C.$-2y^{2}+4y=-2y(y + 2)$
D.$m^{2}n-2mn + n=n(m - 1)^{2}$
A.$x^{2}-1=(x - 1)^{2}$
B.$a^{3}-2a^{2}+a=a^{2}(a - 2)$
C.$-2y^{2}+4y=-2y(y + 2)$
D.$m^{2}n-2mn + n=n(m - 1)^{2}$
答案:
D
7. 辨思维 易错题 已知$a,b$为常数,若$ax + b>0$的解集是$x<\frac{1}{3}$,则$bx - a<0$的解集是( )
A.$x>-3$
B.$x<-3$
C.$x>3$
D.$x<3$
A.$x>-3$
B.$x<-3$
C.$x>3$
D.$x<3$
答案:
B [解析]
∵ax + b>0的解集是x<$\frac{1}{3}$,由于不等号的方向发生了变化,
∴a<0。又
∵−$\frac{b}{a}$=$\frac{1}{3}$,即a = −3b,
∴b>0,不等式bx - a<0,即bx + 3b<0,解得x<−3。故选B。
∵ax + b>0的解集是x<$\frac{1}{3}$,由于不等号的方向发生了变化,
∴a<0。又
∵−$\frac{b}{a}$=$\frac{1}{3}$,即a = −3b,
∴b>0,不等式bx - a<0,即bx + 3b<0,解得x<−3。故选B。
8. 新课标 应用意识 小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:$x - y,a - b,2,x^{2}-y^{2},a,x + y$,分别对应下列六个字:华、我、爱、美、游、中,现将$2a(x^{2}-y^{2})-2b(x^{2}-y^{2})$因式分解,结果呈现的密码信息可能是( )
A.爱我中华
B.我游中华
C.中华美
D.我爱美
A.爱我中华
B.我游中华
C.中华美
D.我爱美
答案:
A [解析]2a(x² - y²) - 2b(x² - y²) = 2(a - b)(x² - y²) = 2(a - b)(x + y)(x - y),信息中的汉字包括:爱、我、中、华,
∴结果呈现的密码信息可能是爱我中华。故选A。
∴结果呈现的密码信息可能是爱我中华。故选A。
9. 小华拿24元钱购买火腿肠和方便面,已知1桶方便面5元,1根火腿肠2元,他买了4桶方便面、$x$根火腿肠,则关于$x$的不等式表示正确的是( )
A.$5\times4 + 2x<24$
B.$5\times4 + 2x\leqslant24$
C.$5x + 2\times4\leqslant24$
D.$5x + 2\times4\geqslant24$
A.$5\times4 + 2x<24$
B.$5\times4 + 2x\leqslant24$
C.$5x + 2\times4\leqslant24$
D.$5x + 2\times4\geqslant24$
答案:
B
10. 辨思维 数形结合 如图,两个正方形边长分别为$a,b$,若$a + b = 10,ab = 18$,则阴影部分的面积为( )【变式训练→B卷T10】

A.21
B.22
C.23
D.24

A.21
B.22
C.23
D.24
答案:
C [解析]如图,三角形②的一条直角边为a - b,另一条直角边为b,因此S三角形② = $\frac{1}{2}$(a - b)b = $\frac{1}{2}$ab - $\frac{1}{2}$b²,S三角形① = $\frac{1}{2}$a²,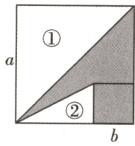
∴S阴影部分 = S大正方形 - S三角形① - S三角形② = $\frac{1}{2}$a² - $\frac{1}{2}$ab + $\frac{1}{2}$b² = $\frac{1}{2}$[(a + b)² - 3ab] = $\frac{1}{2}$×(100 - 54) = 23。故选C。
C [解析]如图,三角形②的一条直角边为a - b,另一条直角边为b,因此S三角形② = $\frac{1}{2}$(a - b)b = $\frac{1}{2}$ab - $\frac{1}{2}$b²,S三角形① = $\frac{1}{2}$a²,

∴S阴影部分 = S大正方形 - S三角形① - S三角形② = $\frac{1}{2}$a² - $\frac{1}{2}$ab + $\frac{1}{2}$b² = $\frac{1}{2}$[(a + b)² - 3ab] = $\frac{1}{2}$×(100 - 54) = 23。故选C。
11. 新考向 跨学科 (扬州三模)“燕山雪花大如席,片片吹落轩辕台.”这是诗仙李白眼里的雪花.单个雪花的质量其实很轻,只有0.000 03 kg左右,数据0.000 03用科学记数法可表示为_______.
答案:
3×10⁻⁵
12. 辨思维 整体思想 (遵义中考)若$a + b = 4,a - b = 2$,则$a^{2}-b^{2}$的值为_______.
答案:
8
13. 在比较$\sqrt{170}$与13的大小关系时,我们可以把它们分别平方,$(\sqrt{170})^{2}=170,13^{2}=169$,依据正数越大,算术平方根越大,得到$\sqrt{170}>13$,请利用上面的方法解答下面的问题:比较大小$\frac{\sqrt{5}}{5}$_______$\frac{\sqrt{6}}{6}$.(填“>”“<”或“=”)
答案:
> [解析]($\frac{\sqrt{5}}{5}$)² = $\frac{1}{5}$,($\frac{\sqrt{6}}{6}$)² = $\frac{1}{6}$。
∵$\frac{1}{5}$>$\frac{1}{6}$,
∴$\frac{\sqrt{5}}{5}$>$\frac{\sqrt{6}}{6}$。
∵$\frac{1}{5}$>$\frac{1}{6}$,
∴$\frac{\sqrt{5}}{5}$>$\frac{\sqrt{6}}{6}$。
14. 辨思维 易错题 (安庆期中)已知关于$x$的不等式组$\begin{cases}\frac{x + 15}{2}>x + 3 \\ 4x + 1>a\end{cases}$.
(1)当$a = 5$时,该不等式组的解集是_______.
(2)若该不等式组有且仅有3个整数解,则$a$的取值范围是_______.
(1)当$a = 5$时,该不等式组的解集是_______.
(2)若该不等式组有且仅有3个整数解,则$a$的取值范围是_______.
答案:
(1)1<x<9
(2)21≤a<25
解不等式$\frac{x + 15}{2}$>3①,得x<9;当a = 5时,4x + 1>5,解得x>1,
∴不等式组的解集是1<x<9。
∵不等式①的解集是x<9,不等式②的解集是x>$\frac{a - 1}{4}$,
∴不等式组的解集为$\frac{a - 1}{4}$<x<9。又
∵该不等式组有且仅有3个整数解,
∴这三个整数解是6,7,8,
∴5≤$\frac{a - 1}{4}$<6,解得21≤a<25。
(1)1<x<9
(2)21≤a<25
解不等式$\frac{x + 15}{2}$>3①,得x<9;当a = 5时,4x + 1>5,解得x>1,
∴不等式组的解集是1<x<9。
∵不等式①的解集是x<9,不等式②的解集是x>$\frac{a - 1}{4}$,
∴不等式组的解集为$\frac{a - 1}{4}$<x<9。又
∵该不等式组有且仅有3个整数解,
∴这三个整数解是6,7,8,
∴5≤$\frac{a - 1}{4}$<6,解得21≤a<25。
15. 计算.
(1)$\sqrt[3]{-1}+\sqrt{9}-\sqrt{1+\frac{24}{25}}$ (2)$(-a)^{2}\cdot(a^{2})^{3}\div a^{5}$
(1)$\sqrt[3]{-1}+\sqrt{9}-\sqrt{1+\frac{24}{25}}$ (2)$(-a)^{2}\cdot(a^{2})^{3}\div a^{5}$
答案:
解:
(1)原式 = −1 + 3 - $\frac{7}{5}$ = $\frac{3}{5}$。
(2)原式 = a²·a⁶÷a⁵ = a⁸÷a⁵ = a³。
(1)原式 = −1 + 3 - $\frac{7}{5}$ = $\frac{3}{5}$。
(2)原式 = a²·a⁶÷a⁵ = a⁸÷a⁵ = a³。
16. 分解因式.
(1)$x^{4}y^{8}-x^{2}y^{4}z^{2}$ (2)$3a^{2}-12ab + 12b^{2}$
(1)$x^{4}y^{8}-x^{2}y^{4}z^{2}$ (2)$3a^{2}-12ab + 12b^{2}$
答案:
解:
(1)原式 = x²y⁴(x²y² - x²) = x²y⁴(xy² + x)(xy² - x)。
(2)原式 = 3(a² - 4ab + 4b²) = 3(a - 2b)²。
(1)原式 = x²y⁴(x²y² - x²) = x²y⁴(xy² + x)(xy² - x)。
(2)原式 = 3(a² - 4ab + 4b²) = 3(a - 2b)²。
17.(广西中考)解不等式组$\begin{cases}3x - 5<x + 1 \\ \frac{3x - 4}{6}\leqslant\frac{2x - 1}{3}\end{cases}$,并在数轴上表示出不等式组的解集.
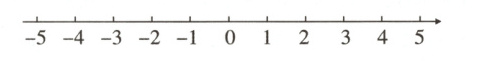
答案:
解:$\begin{cases}3x - 5<x + 1 ①\\\frac{3x - 4}{6}≤\frac{2x - 1}{3} ②\end{cases}$,解不等式①,得x<3;解不等式②,得x≥−2,
∴不等式组的解集为−2≤x<3。在数轴上表示如下:
∴不等式组的解集为−2≤x<3。在数轴上表示如下:
18.(六安期中)先化简,再求值:$(-3x - 2)(2 - 3x)-(3x - 4)^{2}$,其中$\sqrt{5}-2<x<\sqrt{3}$,且$x$为整数.
答案:
解:(x - 16)(x - 1) - (x - 1)² = x² - x - 16x + 16 - (x² - 2x + 1) = x² - 17x + 16 - x² + 2x - 1 = -15x + 15。
∵$\sqrt{3}$<x<$\sqrt{5}$,且x为整数,
∴x = 2,当x = 2时,原式 = -15×2 + 15 = -15。
∵$\sqrt{3}$<x<$\sqrt{5}$,且x为整数,
∴x = 2,当x = 2时,原式 = -15×2 + 15 = -15。
19. 如图,在一个边长为$2a + b$的大正方形纸片中,剪去一个长为$2a + b$、宽为$a - b$的长方形和一个边长为$a - b$的小正方形.
(1)用含$a,b$的式子表示阴影部分的面积.(结果化为最简)
(2)当$a = 5,b = 2$时,求阴影部分的面积.

(1)用含$a,b$的式子表示阴影部分的面积.(结果化为最简)
(2)当$a = 5,b = 2$时,求阴影部分的面积.

答案:
解:
(1)阴影部分的面积为(2a + b)² - (2a + b)(a - b) - (a - b)² = 4a² + 4ab + b² - (2a² - 2ab + ab - b²) - (a² - 2ab + b²) = 4a² + 4ab + b² - 2a² + 2ab - ab + b² - a² + 2ab - b² = a² + 7ab + b²。
(2)当a = 5,b = 2时,原式 = 25 + 7×5×2 + 4 = 99,即阴影部分的面积为99。
(1)阴影部分的面积为(2a + b)² - (2a + b)(a - b) - (a - b)² = 4a² + 4ab + b² - (2a² - 2ab + ab - b²) - (a² - 2ab + b²) = 4a² + 4ab + b² - 2a² + 2ab - ab + b² - a² + 2ab - b² = a² + 7ab + b²。
(2)当a = 5,b = 2时,原式 = 25 + 7×5×2 + 4 = 99,即阴影部分的面积为99。
20. 新课标 运算能力 (安庆期中)已知$2x + 1$的算术平方根是3,$-3x + y + 1$的立方根是-2.
(1)求$x$和$y$的值.
(2)用四则运算的加、减、乘、除定义一个新运算:$a\oplus b = ax - by$.若$m$满足$m\oplus2\leqslant0$,且$3m\oplus(-8)>0$,化简:$|m - \sqrt{5}|+|m + 2|$.
(1)求$x$和$y$的值.
(2)用四则运算的加、减、乘、除定义一个新运算:$a\oplus b = ax - by$.若$m$满足$m\oplus2\leqslant0$,且$3m\oplus(-8)>0$,化简:$|m - \sqrt{5}|+|m + 2|$.
答案:
解:
(1)由题意可得,$\begin{cases}2 - x + 3 + x + 1 + y = 9 + 1\\-8 = -8\end{cases}$,解得$\begin{cases}x = 4\\y = 3\end{cases}$,
∴x = 4,y = 3。
(2)
∵x = 4,y = 3,
∴ab = 4a - 3b,
∴由题意可得,$\begin{cases}4m + 2 - 6m ≤ 4\\2m - 2>0\end{cases}$,解得−2<m≤$\frac{3}{2}$,
∴原式 = $\sqrt{5 - m} + m + 2$ = $\sqrt{5} + 2$。
(1)由题意可得,$\begin{cases}2 - x + 3 + x + 1 + y = 9 + 1\\-8 = -8\end{cases}$,解得$\begin{cases}x = 4\\y = 3\end{cases}$,
∴x = 4,y = 3。
(2)
∵x = 4,y = 3,
∴ab = 4a - 3b,
∴由题意可得,$\begin{cases}4m + 2 - 6m ≤ 4\\2m - 2>0\end{cases}$,解得−2<m≤$\frac{3}{2}$,
∴原式 = $\sqrt{5 - m} + m + 2$ = $\sqrt{5} + 2$。
六、(本题满分12分)
21. 新教材 变式题 (合肥期中)观察下列等式,并回答问题.【变式训练→B卷T22】
$4\times1=2^{2}-0^{2}$,
$4\times2=3^{2}-1^{2}$,
$4\times3=4^{2}-2^{2}$,
…
(1)将2 024写成两整数平方差的形式:$2024 = 4\times$_______$=$_______ - _______.
(2)用含有字母$n(n\geqslant1$的整数)的等式表示这一规律,并用已学的知识验证这一规律.
(3)相邻的两个整数的平方差是4的倍数吗?请说说你的理由.
21. 新教材 变式题 (合肥期中)观察下列等式,并回答问题.【变式训练→B卷T22】
$4\times1=2^{2}-0^{2}$,
$4\times2=3^{2}-1^{2}$,
$4\times3=4^{2}-2^{2}$,
…
(1)将2 024写成两整数平方差的形式:$2024 = 4\times$_______$=$_______ - _______.
(2)用含有字母$n(n\geqslant1$的整数)的等式表示这一规律,并用已学的知识验证这一规律.
(3)相邻的两个整数的平方差是4的倍数吗?请说说你的理由.
答案:
解:
(1)506² - 505² = (506 + 505)×(506 - 505) = 1011;507² - 505² = (507 + 505)×(507 - 505) = 2024。
(2)4n = (n + 1)² - (n - 1)²,验证如下:
∵(n + 1)² - (n - 1)² = n² + 2n + 1 - (n² - 2n + 1) = 4n,
∴4n = (n + 1)² - (n - 1)²。
(3)相邻的两个整数的平方差不是4的倍数,理由如下:设相邻的两个整数分别为a,a + 1,其中a为整数。
∵(a + 1)² - a² = a² + 2a + 1 - a² = 2a + 1,2a + 1为奇数,不是4的倍数,
∴相邻的两个整数的平方差不是4的倍数。
解:
(1)506² - 505² = (506 + 505)×(506 - 505) = 1011;507² - 505² = (507 + 505)×(507 - 505) = 2024。
(2)4n = (n + 1)² - (n - 1)²,验证如下:
∵(n + 1)² - (n - 1)² = n² + 2n + 1 - (n² - 2n + 1) = 4n,
∴4n = (n + 1)² - (n - 1)²。
(3)相邻的两个整数的平方差不是4的倍数,理由如下:设相邻的两个整数分别为a,a + 1,其中a为整数。
∵(a + 1)² - a² = a² + 2a + 1 - a² = 2a + 1,2a + 1为奇数,不是4的倍数,
∴相邻的两个整数的平方差不是4的倍数。

七、(本题满分12分)
22.(桂林中考)为丰富学生的体育活动,某校购买了50个A类足球和25个B类足球共花费7 500元,已知购买1个B类足球比购买1个A类足球多花30元.
(1)求购买1个A类足球和1个B类足球各需要多少元.
(2)通过全校师生的共同努力,今年该校被评为“足球特色学校”,学校计划用不超过4 800元的经费再次购买A类足球和B类足球共50个,若单价不变,则本次至少可以购买多少个A类足球?
22.(桂林中考)为丰富学生的体育活动,某校购买了50个A类足球和25个B类足球共花费7 500元,已知购买1个B类足球比购买1个A类足球多花30元.
(1)求购买1个A类足球和1个B类足球各需要多少元.
(2)通过全校师生的共同努力,今年该校被评为“足球特色学校”,学校计划用不超过4 800元的经费再次购买A类足球和B类足球共50个,若单价不变,则本次至少可以购买多少个A类足球?
答案:
解:
(1)设购买1个A类足球需要x元,购买1个B类足球需要y元。由题意,得$\begin{cases}y - x = 30\\50x + 25y = 7500\end{cases}$,解得$\begin{cases}x = 90\\y = 120\end{cases}$。答:购买1个A类足球需要90元,购买1个B类足球需要120元。
(2)设购买m个A类足球,则购买(50 - m)个B类足球。依题意,得90m + 120(50 - m) ≤ 4800,解得m ≥ 40。答:本次至少可以购买40个A类足球。
(1)设购买1个A类足球需要x元,购买1个B类足球需要y元。由题意,得$\begin{cases}y - x = 30\\50x + 25y = 7500\end{cases}$,解得$\begin{cases}x = 90\\y = 120\end{cases}$。答:购买1个A类足球需要90元,购买1个B类足球需要120元。
(2)设购买m个A类足球,则购买(50 - m)个B类足球。依题意,得90m + 120(50 - m) ≤ 4800,解得m ≥ 40。答:本次至少可以购买40个A类足球。
八、(本题满分14分)
23. 新考向 阅读理解 (马鞍山期中)阅读理解并解答:
[方法呈现]
(1)我们把多项式$a^{2}+2ab + b^{2}$及$a^{2}-2ab + b^{2}$叫作完全平方式.在运用完全平方公式进行因式分解时,关键是判断这个多项式是不是一个完全平方式,同样地,把一个多项式进行局部因式分解可以解决求代数式值的最小(或最大)值问题.
例如:$x^{2}+2x + 3=(x^{2}+2x + 1)+2=(x + 1)^{2}+2$,
$\because(x + 1)^{2}\geqslant0$,
$\therefore(x + 1)^{2}+2\geqslant2$.
则代数式$x^{2}+2x + 3$的最小值是_______,这时相应的$x$的值是_______.
[尝试应用]
(2)仿照上述方法求代数式$-x^{2}+14x + 10$的最小(或最大)值,并写出相应的$x$的值.
23. 新考向 阅读理解 (马鞍山期中)阅读理解并解答:
[方法呈现]
(1)我们把多项式$a^{2}+2ab + b^{2}$及$a^{2}-2ab + b^{2}$叫作完全平方式.在运用完全平方公式进行因式分解时,关键是判断这个多项式是不是一个完全平方式,同样地,把一个多项式进行局部因式分解可以解决求代数式值的最小(或最大)值问题.
例如:$x^{2}+2x + 3=(x^{2}+2x + 1)+2=(x + 1)^{2}+2$,
$\because(x + 1)^{2}\geqslant0$,
$\therefore(x + 1)^{2}+2\geqslant2$.
则代数式$x^{2}+2x + 3$的最小值是_______,这时相应的$x$的值是_______.
[尝试应用]
(2)仿照上述方法求代数式$-x^{2}+14x + 10$的最小(或最大)值,并写出相应的$x$的值.
答案:
解:
(1)2, - 1
(2) - x² + 14x + 10 = - (x² - 14x + 49 - 49) + 10 = - (x - 7)² + 59。
∵ - (x - 7)² ≤ 0,
∴ - (x - 7)² + 59 ≤ 59,故代数式 - x² + 14x + 10的最大值为59,相应的x的值为7。
(1)2, - 1
(2) - x² + 14x + 10 = - (x² - 14x + 49 - 49) + 10 = - (x - 7)² + 59。
∵ - (x - 7)² ≤ 0,
∴ - (x - 7)² + 59 ≤ 59,故代数式 - x² + 14x + 10的最大值为59,相应的x的值为7。
1.(黄山期中)实数$|-\sqrt{6}|$,0,-2,$-\sqrt{5}$中,最小的数是( )
A. $|-\sqrt{6}|$
B. 0
C. -2
D. $-\sqrt{5}$
A. $|-\sqrt{6}|$
B. 0
C. -2
D. $-\sqrt{5}$
答案:
D
2.(六安期中)下列计算正确的是( )
A. $a^{2}\cdot a^{3}=a^{6}$
B. $a^{6}\div a^{-2}=a^{4}$
C. $(2a + b)^{2}=4a^{2}+b^{2}$
D. $(-2ab^{2})^{3}=-8a^{3}b^{6}$
A. $a^{2}\cdot a^{3}=a^{6}$
B. $a^{6}\div a^{-2}=a^{4}$
C. $(2a + b)^{2}=4a^{2}+b^{2}$
D. $(-2ab^{2})^{3}=-8a^{3}b^{6}$
答案:
D
3. 将不等式组$\begin{cases}2x - 6\leqslant0 \\ x + 4>0\end{cases}$的解集表示在数轴上,下面表示正确的是( )
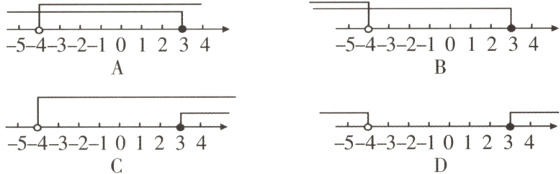
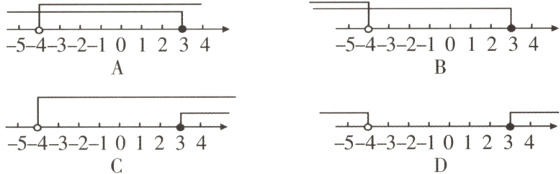
答案:
A
4.(淮北期中)下列因式分解正确的是( )
A. $2b^{2}-8b + 8=2(b - 2)^{2}$
B. $ay^{2}-2ay + y=y(ay - 2a)$
C. $a^{2}+a - 3=a(a + 1)-3$
D. $3x^{3}y-xy^{2}=3xy(x^{2}-y)$
A. $2b^{2}-8b + 8=2(b - 2)^{2}$
B. $ay^{2}-2ay + y=y(ay - 2a)$
C. $a^{2}+a - 3=a(a + 1)-3$
D. $3x^{3}y-xy^{2}=3xy(x^{2}-y)$
答案:
A
5.(临沂中考)已知$a>b$,下列结论:①$a^{2}>ab$;②$a^{2}>b^{2}$;③若$b<0$,则$a + b<2b$;④若$b>0$,则$\frac{1}{a}<\frac{1}{b}$. 其中正确的个数是( )
A. 1
B. 2
C. 3
D. 4
A. 1
B. 2
C. 3
D. 4
答案:
A [解析]
∵a>b,
∴当a>0时,a²>ab;当a<0时,a²<ab,故①结论错误.
∵a>b,
∴当b>0时,|a|>|b|,a²>b²;当a<0时,|a|<|b|,a²<b²,故②结论错误.
∵a>b,b<0,
∴a+b>2b,故③结论错误.
∵a>b,b>0,
∴a>b>0,
∴$\frac{1}{a}$<$\frac{1}{b}$,故④结论正确.故选A.
∵a>b,
∴当a>0时,a²>ab;当a<0时,a²<ab,故①结论错误.
∵a>b,
∴当b>0时,|a|>|b|,a²>b²;当a<0时,|a|<|b|,a²<b²,故②结论错误.
∵a>b,b<0,
∴a+b>2b,故③结论错误.
∵a>b,b>0,
∴a>b>0,
∴$\frac{1}{a}$<$\frac{1}{b}$,故④结论正确.故选A.
6. 辨思维 整体思想(聊城中考)关于$x$,$y$的方程组$\begin{cases}2x - y=2k - 3 \\ x - 2y=k\end{cases}$的解中$x$与$y$的和不小于5,则$k$的取值范围为( )
A. $k\geqslant8$
B. $k>8$
C. $k\leqslant8$
D. $k<8$
A. $k\geqslant8$
B. $k>8$
C. $k\leqslant8$
D. $k<8$
答案:
A [解析]把两个方程相减,可得x+y=k - 3,根据题意得k - 3≥5,解得k≥8,
∴k的取值范围为k≥8.
∴k的取值范围为k≥8.
7. 新考向 开放题(合肥期中)已知$(x + a)(x + b)=x^{2}+mx + 12$,$m$,$a$,$b$都是整数,那么$m$的值有( )种可能.
A. 4
B. 5
C. 6
D. 8
A. 4
B. 5
C. 6
D. 8
答案:
C [解析]
∵(x+a)(x+b)=x²+mx+12=x²+(a+b)x+ab,
∴a+b=m,ab=12.
∵m,a,b都是整数,
∴当a=3,b=4时,m=a+b=7;当a=-3,b=-4时,m=a+b=-7;当a=2,b=6时,m=a+b=8;当a=-2,b=-6时,m=a+b=-8;当a=1,b=12时,m=a+b=13;当a=-1,b=-12时,m=a+b=-13,则m的值有6种可能.故选C.
∵(x+a)(x+b)=x²+mx+12=x²+(a+b)x+ab,
∴a+b=m,ab=12.
∵m,a,b都是整数,
∴当a=3,b=4时,m=a+b=7;当a=-3,b=-4时,m=a+b=-7;当a=2,b=6时,m=a+b=8;当a=-2,b=-6时,m=a+b=-8;当a=1,b=12时,m=a+b=13;当a=-1,b=-12时,m=a+b=-13,则m的值有6种可能.故选C.
查看更多完整答案,请扫码查看


