《2025年海淀单元测试AB卷七年级数学下册沪科版》

20. 辨思维 数形结合 如图所示，数轴的正半轴上有A，B，C三点，点A，B分别表示1，$\sqrt{2}$，且点B到点A的距离与点C到原点的距离相等，设点C所表示的数为$x$.【变式训练→B卷T19】

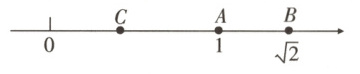
(1)请你写出数$x$的值.
(2)求$(x - \sqrt{2})^{2}$的立方根.

答案： 解:
(1)$\because$点A，B分别表示1，$\sqrt{2}$，$\therefore AB=\sqrt{2}-1$。设点C表示的数为x，$\because$点C到点A的距离与点C到原点的距离相等，$\therefore |x - 1| = |x|$，解得x = $\frac{\sqrt{2}}{2}$。
(2)$\because x = \frac{\sqrt{2}}{2}$，$\therefore (x - \sqrt{2})² = (\frac{\sqrt{2}}{2}-\sqrt{2})² = (-\frac{\sqrt{2}}{2})²=\frac{1}{2}$，$\therefore (x - \sqrt{2})²$的立方根为$\sqrt[3]{\frac{1}{2}}$。

六、（本题满分12分）
21. 公园里有一个边长为8米的正方形花坛，如图所示，现在想扩大花坛的面积. 要使花坛的面积增加80平方米后仍然是正方形，边长应该延长多少米？

答案： 解:设边长应该延长x米。根据题意，得(x + 8)² = 8² + 80，即(x + 8)² = 144。$\because$花坛的边长不能为负，$\therefore x + 8 = \sqrt{144}=12$，$\therefore x = 4$，即边长应该延长4米。