《2025年亮点给力新情境素养卷六年级数学下册人教版》

3. 如图，在一个由圆锥和圆柱组成的高为8 cm的玻璃容器中加入一些水，并盖上盖子，水面高6 cm，圆柱和圆锥的高相等。当把这个玻璃容器倒过来时，水面高多少厘米？(6分)

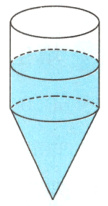
答案： $6 - 8\div2+8\div2\div3=\frac{10}{3}(cm)$

4. 如图，有一卷紧紧缠绕在一起的塑料薄膜，薄膜卷的底面直径为20 cm，中间有一底面直径为8 cm的纸筒。已知薄膜的厚度为0.02 cm，薄膜卷展开后的长度是多少米？(6分)

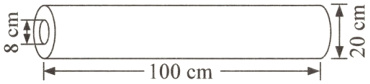
答案： $20\div2 = 10(cm)$ $8\div2 = 4(cm)$
$3.14\times(10^{2}-4^{2})\times100 = 26376(cm^{3})$
$26376\div100\div0.02 = 13188(cm)$
$13188\ cm = 131.88\ m$
[解析:由题图可知,缠绕在一起的塑料薄膜是空心圆柱形,已知底面外半径是$20\div2 = 10(cm)$,底面内半径是$8\div2 = 4(cm)$,高是$100\ cm$,根据圆柱体积公式求出塑料薄膜的体积为$3.14\times(10^{2}-4^{2})\times100 = 26376(cm^{3})$,塑料薄膜卷展开后为长方体,它的厚度即是长方体的高,空心圆柱的高即是长方体的宽,要求塑料薄膜卷展开后的长度,就是求长方体的长。因为塑料薄膜卷展开前后的体积是不变的,所以塑料薄膜卷展开后的长度为$26376\div100\div0.02 = 13188(cm)$,换算单位后是$131.88\ m$。]

## 六、拓展提优。（共10分）
1. 一个长方体容器中注满了水。第一次把一个小钢球浸没在水中；第二次取出小钢球后，将一个钢制圆锥浸没在水中；第三次取出圆锥，把一个钢制圆柱浸没在水中，并且这个圆柱和圆锥等底等高。已知第一次溢出的水是6立方厘米，第二次溢出的水是9立方厘米，则第三次溢出的水是( )立方厘米。（4分）

答案： 30 [解析:取出小钢球后,这时容器中就会空出一部分空间出来,这个空间就是小钢球的体积6立方厘米,所以把圆锥浸没在水中时,它先占满这6立方厘米,再溢出水9立方厘米,由此可以得出圆锥的体积是$6 + 9 = 15$(立方厘米)。因为圆柱与圆锥等底等高,所以圆柱的体积是$15\times3 = 45$(立方厘米)。当把圆柱浸没在水中时,它先占满15立方厘米,再溢出水$45 - 15 = 30$(立方厘米)。]

2. 新素养 推理意识 有甲、乙两个分别是圆锥形和圆柱形的容器，它们底面半径的比是3：4，高的比是4：5。现在每次用甲容器装满水倒入乙容器中，这样进行若干次后，乙容器水满了，甲容器中还剩余120毫升水。甲、乙容器的容积各是多少毫升？（6分）

答案：  $(3.14\times3^{2}\times4\times\frac{1}{3}):(3.14\times4^{2}\times5)=3:20$
$3\times7 = 21$ $21 - 20 = 1$
甲容器:$120\times3 = 360$(毫升)
乙容器:$120\times20 = 2400$(毫升)
[解析:由甲、乙两个容器底面半径的比是$3:4$,高的比是$4:5$,可求出甲容器的容积:乙容器的容积$=(3.14\times3^{2}\times4\times\frac{1}{3}):(3.14\times4^{2}\times5)=3:20$。假设乙容器能装20份水,则甲容器能装3份水,甲容器装满水倒7次将乙容器倒满,此时甲容器留下1份水,即120毫升,因此甲容器的容积是$120\times3 = 360$(毫升),乙容器的容积是$120\times20 = 2400$(毫升)。]