《2024年轻轻松松九年级数学全一册冀教版》

4. 图30 - 4 - 6是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称。AB//x轴，AB = 4 cm，最低点C在x轴上，高CH = 1 cm，BD = 2 cm，则右轮廓线DFE所在抛物线的函数表达式为( )
图30 - 4 - 6
A. y = $\frac{1}{4}$(x + 3)²
B. y = -$\frac{1}{4}$(x + 3)²
C. y = $\frac{1}{4}$(x - 3)²
D. y = -$\frac{1}{4}$(x - 3)²

答案： C 解析:$\because$高$CH = 1\text{ cm}$,$BD = 2\text{ cm}$,而$B$,$D$关于$y$轴对称,$\therefore D$点坐标为$(1,1)$.$\because AB// x$轴,$AB = 4\text{ cm}$,最低点$C$在$x$轴上,$\therefore A$,$B$关于直线$CH$对称,$\therefore$左边抛物线的顶点$C$的坐标为$(-3,0)$,$\therefore$右边抛物线的顶点$F$的坐标为$(3,0)$.设右边抛物线的表达式为$y = a(x - 3)^{2}$,把$D(1,1)$代入,得$1 = a\times(1 - 3)^{2}$,解得$a = \frac{1}{4}$,故右边抛物线的表达式为$y = \frac{1}{4}(x - 3)^{2}$.

二、填空题
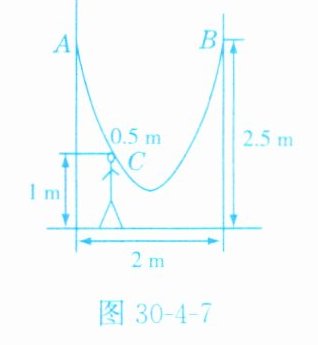
5. 如图30 - 4 - 7，小明的父亲在相距2 m的两棵树间拴了一根绳子，给他做了一个简易的秋千，拴绳子的地方距地面都是2.5 m，绳子自然下垂呈抛物线状，身高1 m的小明距较近的那棵树0.5 m时，头部刚好接触到绳子，则绳子的最低点与地面的距离为________米。

答案：
0.5 解析:以左边树与地面的交点为原点,地面水平线为$x$轴,左边树所在直线为$y$轴建立平面直角坐标系,如图 D - 30 - 8,由图像可得$A(0,2.5)$,$B(2,2.5)$,$C(0.5,1)$.设函数表达式为$y = ax^{2}+bx + c$,把$A$,$B$,$C$三点的坐标分别代入,得$\begin{cases}c = 2.5,\\4a + 2b + c = 2.5,\\0.25a + 0.5b + c = 1,\end{cases}$解得$\begin{cases}a = 2,\\b = - 4,\\c = 2.5.\end{cases}$$\therefore y = 2x^{2}-4x + 2.5 = 2(x - 1)^{2}+0.5$.$\because 2＞0$,$\therefore$当$x = 1$时,$y_{最小值}=0.5\text{ m}$.

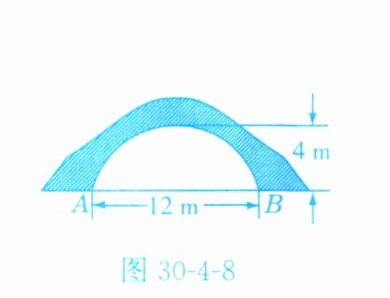
6. 如图30 - 4 - 8，一座拱桥，当水面宽AB为12 m时，桥洞顶部离水面4 m，已知桥洞的拱形是抛物线，以水平方向为x轴，建立平面直角坐标系，若选取点A为坐标原点时的抛物线表达式是y = -$\frac{1}{9}$(x - 6)² + 4，则选取点B为坐标原点时的抛物线表达式是__________。

答案：
$y = -\frac{1}{9}(x + 6)^{2}+4$(或$y = -\frac{1}{9}x^{2}-\frac{4}{3}x$) 解析:以点$B$为坐标原点,以$AB$所在直线为$x$轴,建立直角坐标系,如图 D - 30 - 9,可设抛物线的表达式为$y = a(x + 6)^{2}+4$,将$A(-12,0)$代入,得$0 = a(-12 + 6)^{2}+4$,解得$a = -\frac{1}{9}$,$\therefore$选取点$B$为坐标原点时的抛物线的表达式是$y = -\frac{1}{9}(x + 6)^{2}+4 = -\frac{1}{9}x^{2}-\frac{4}{3}x$. 故答案为$y = -\frac{1}{9}(x + 6)^{2}+4$或$y = -\frac{1}{9}x^{2}-\frac{4}{3}x$.

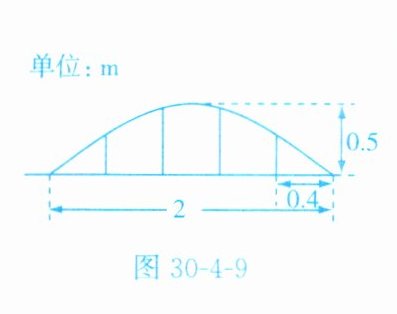
7. 某公园草坪的防护栏由100段形状相同的抛物线形构件组成，为了牢固起见，每段护栏需要间距0.4 m加设一根不锈钢的支柱，防护栏的最高点距底部0.5 m(如图30 - 4 - 9)，则这条防护栏需要不锈钢支柱的总长度至少为________m。

答案：
160 解析:如图 D - 30 - 10,建立直角坐标系,由题意,得$B(0,0.5)$,$C(1,0)$,设抛物线的表达式为$y = ax^{2}+c$.把点$B(0,0.5)$,$C(1,0)$代入$y = ax^{2}+c$中,得$a = -\frac{1}{2}$,$c = \frac{1}{2}$,$\therefore$抛物线的表达式为$y = -\frac{1}{2}x^{2}+\frac{1}{2}$.当$x = 0.2$时,$y = 0.48$,当$x = 0.6$时,$y = 0.32$,$\therefore B_{1}C_{1}+B_{2}C_{2}+B_{3}C_{3}+B_{4}C_{4}=2\times(0.48 + 0.32)=1.6(\text{m})$.$\therefore$所需不锈钢支柱的总长度为$1.6\times100 = 160(\text{m})$.

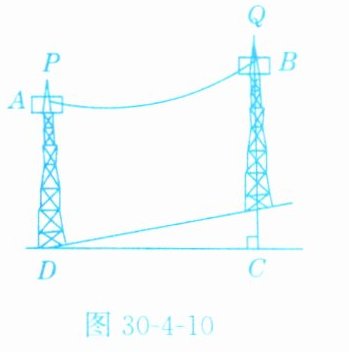
8. 某种电缆在空中架设时，两端挂起的电缆下垂都近似抛物线y = $\frac{1}{100}$x²的形状。今在一个坡度为1∶5的斜坡上，沿水平距离间隔50 m架设两固定电缆的位置离地面高度为20 m的塔柱(如图30 - 4 - 10)，这种情况下，在竖直方向上，下垂的电缆与地面的最近距离为________米。

答案：
13.75 解析:如图 D - 30 - 11,以点$D$为原点,$DC$方向为$x$轴建立直角坐标系,设抛物线的表达式为$y = \frac{1}{100}x^{2}+bx + c$,$\because\frac{EC}{DC}=\frac{1}{5}$,$\frac{EC}{50}=\frac{1}{5}$,$\therefore EC = 10$,$\therefore BC = 30$.$\therefore A(0,20)$,$B(50,30)$,把点$A$,$B$的坐标分别代入抛物线表达式,得$\begin{cases}c = 20,\\25 + 50b + c = 30,\end{cases}$解得$\begin{cases}b = -\frac{3}{10},\\c = 20,\end{cases}$$\therefore$抛物线的表达式为$y = \frac{1}{100}x^{2}-\frac{3}{10}x + 20$.$\because$斜坡的坡度为$1:5$,$\therefore$斜坡所在直线的表达式为$y = \frac{1}{5}x$.设一条与$x$轴垂直的直线$x = m$与抛物线交于点$M$,与斜坡交于点$G$,则$MG = \frac{1}{100}m^{2}-\frac{3}{10}m + 20-\frac{1}{5}m = \frac{1}{100}(m - 25)^{2}+13.75$,$\therefore$当$m = 25$时,$MG$的最小值为$13.75$,即下垂的电缆与地面的最近距离为$13.75\text{ m}$.

三、解答题
9. 如图30 - 4 - 11，某足球运动员站在点O处练习射门，将足球从离地面0.5 m的A处正对球门踢出(点A在y轴上)，足球的飞行高度y(单位：m)与飞行时间t(单位：s)之间满足函数关系y = at² + 5t + c，已知足球飞行0.8 s时，离地面的高度为3.5 m。
图30 - 4 - 11
(1)足球飞行的时间是多少时，足球离地面最高？最大高度是多少？
(2)若足球飞行的水平距离x(单位：m)与飞行时间t(单位：s)之间具有函数关系x = 10t，已知球门的高度为2.44 m，如果该运动员正对球门射门时，离球门的水平距离为28 m，他能否将球直接射入球门？

答案： 解:
(1)由题意,得函数$y = at^{2}+5t + c$的图像经过点$(0,0.5)$,$(0.8,3.5)$,$\therefore\begin{cases}0.5 = c,\\3.5 = 0.8^{2}a + 5\times0.8 + c,\end{cases}$解得$\begin{cases}a = -\frac{25}{16},\\c = \frac{1}{2},\end{cases}$$\therefore$抛物线的表达式为$y = -\frac{25}{16}t^{2}+5t+\frac{1}{2}$,$\therefore$当$t = \frac{8}{5}$时,$y_{最大值}=4.5$.
(2)把$x = 28$代入$x = 10t$,得$t = 2.8$,当$t = 2.8$时,$y = -\frac{25}{16}\times2.8^{2}+5\times2.8+\frac{1}{2}=2.25＜2.44$,$\therefore$他能将球直接射入球门.