第168页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
- 第206页
- 第207页
- 第208页
- 第209页
- 第210页
- 第211页
- 第212页
- 第213页
- 第214页
- 第215页
- 第216页
- 第217页
- 第218页
- 第219页
- 第220页
- 第221页
- 第222页
- 第223页
- 第224页
- 第225页
- 第226页
- 第227页
- 第228页
- 第229页
- 第230页
- 第231页
- 第232页
- 第233页
- 第234页
- 第235页
- 第236页
- 第237页
6.在平面直角坐标系xOy中,以点(-3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
A.与x轴相交,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
答案:
C 解析:
∵点( - 3,4)到x轴的距离为4个单位长度,到y轴的距离为3个单位长度,
∴该圆与x轴相切,与y轴相交.
∵点( - 3,4)到x轴的距离为4个单位长度,到y轴的距离为3个单位长度,
∴该圆与x轴相切,与y轴相交.
二、填空题
答案:
7.两个同心圆的半径分别为3 cm和6 cm,大圆的弦MN=6$\sqrt{3}$ cm,则MN与小圆的位置关系是________.
答案:
相切 解析:如图D - 29 - 7,过点O作OA⊥MN于点A,连接OM,则MA = $\frac{1}{2}$MN = $\frac{1}{2}$×6$\sqrt{3}$ = 3$\sqrt{3}$(cm). 在Rt△OMA中,OA = $\sqrt{OM^{2}-MA^{2}}$ = $\sqrt{6^{2}-(3$\sqrt{3}$)^{2}}$ = 3(cm). 又
∵小圆半径为3 cm,
∴MN与小圆相切.

相切 解析:如图D - 29 - 7,过点O作OA⊥MN于点A,连接OM,则MA = $\frac{1}{2}$MN = $\frac{1}{2}$×6$\sqrt{3}$ = 3$\sqrt{3}$(cm). 在Rt△OMA中,OA = $\sqrt{OM^{2}-MA^{2}}$ = $\sqrt{6^{2}-(3$\sqrt{3}$)^{2}}$ = 3(cm). 又
∵小圆半径为3 cm,
∴MN与小圆相切.

8.如图29 - 2 - 7,⊙A的圆心坐标为A(0,4),若⊙A的半径为3,则直线l:y=x与⊙A的位置关系是________.
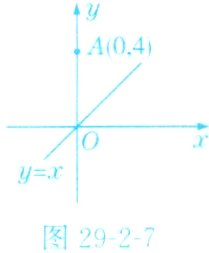

答案:
相交 解析:如图D - 29 - 8,过点A作AB⊥l,垂足是B.
在Rt△AOB中,∠AOB = 45°,
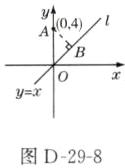
∴AB = OA·sin 45° = 4×$\frac{\sqrt{2}}{2}$ = 2$\sqrt{2}$<3,
∴直线l:y = x与⊙A相交.
相交 解析:如图D - 29 - 8,过点A作AB⊥l,垂足是B.
在Rt△AOB中,∠AOB = 45°,

∴AB = OA·sin 45° = 4×$\frac{\sqrt{2}}{2}$ = 2$\sqrt{2}$<3,
∴直线l:y = x与⊙A相交.
9.如图29 - 2 - 8,△AOB中,∠O=90°,AO=8 cm,BO=6 cm,点C从A点出发,在边AO上以2 cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5 cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了________s时,以C点为圆心,1.5 cm为半径的圆与直线EF相切.
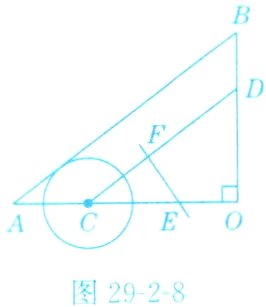

答案:
$\frac{17}{8}$ 解析:当以点C为圆心,1.5 cm为半径的圆与直线EF相切时,此时,CF = 1.5,
∵AC = 2t,BD = $\frac{3}{2}$t,
∴OC = 8 - 2t,OD = 6 - $\frac{3}{2}$t.
∵点E是OC的中点,
∴CE = $\frac{1}{2}$OC = 4 - t.
∵∠EFC = ∠O = 90°,∠ECF = ∠DCO,
∴△EFC∽△DOC,
∴$\frac{EF}{OD}$ = $\frac{CF}{OC}$,
∴EF = $\frac{3OD}{2OC}$ = $\frac{3(6 - $\frac{3}{2}$t)}{2(8 - 2t)}$ = $\frac{9}{8}$.
由勾股定理可知CE² = CF² + EF²,
∴(4 - t)² = ($\frac{3}{2}$)² + ($\frac{9}{8}$)²,
解得t = $\frac{17}{8}$或t = $\frac{47}{8}$.
∵0≤t≤4,
∴t = $\frac{17}{8}$.
∵AC = 2t,BD = $\frac{3}{2}$t,
∴OC = 8 - 2t,OD = 6 - $\frac{3}{2}$t.
∵点E是OC的中点,
∴CE = $\frac{1}{2}$OC = 4 - t.
∵∠EFC = ∠O = 90°,∠ECF = ∠DCO,
∴△EFC∽△DOC,
∴$\frac{EF}{OD}$ = $\frac{CF}{OC}$,
∴EF = $\frac{3OD}{2OC}$ = $\frac{3(6 - $\frac{3}{2}$t)}{2(8 - 2t)}$ = $\frac{9}{8}$.
由勾股定理可知CE² = CF² + EF²,
∴(4 - t)² = ($\frac{3}{2}$)² + ($\frac{9}{8}$)²,
解得t = $\frac{17}{8}$或t = $\frac{47}{8}$.
∵0≤t≤4,
∴t = $\frac{17}{8}$.
10.圆心O到直线l的距离为d,⊙O的半径为R.若d,R是方程x²-9x+20=0的两根,且直线与圆的位置关系是相交,则d,R的值分别为________;若d,R是方程x²-4x+m=0的两个根,且直线l与⊙O相切,则m的值为________.
答案:
4,5 4 解析:若直线与圆相交,则d<R,方程的两个根为4,5,则d = 4,R = 5. 若直线与圆相切,则d = R,则方程有两个相等的实数根,则( - 4)² - 4m = 0,则m = 4.
三、解答题
答案:
11.如图29 - 2 - 9,已知∠MON=30°,在ON上有一点P,OP=5 cm,若以P点为圆心,以R为半径作圆,试求圆的半径R的取值范围,使
(1)射线OM与⊙P只有一个公共点.

(2)射线OM与⊙P有两个公共点.
(1)射线OM与⊙P只有一个公共点.

(2)射线OM与⊙P有两个公共点.
答案:
解:
(1)当射线OM与⊙P相切时,射线OM与⊙P只有一个公共点,过点P作PA⊥OM于A(图略),则在Rt△AOP中,PA = OP·sin 30° = 5×$\frac{1}{2}$ = 2.5(cm).
∴当R = 2.5 cm时,射线OM与⊙P只有一个公共点.
当射线OM与⊙P相交时,则必须R>2.5 cm.
又
∵点O在⊙P内,
∴R>OP,即R>5 cm.
∴当R = 2.5 cm或R>5 cm时,射线OM与⊙P只有一个公共点.
(2)当射线OM与⊙P相交时,则必须R>2.5 cm.
又
∵点O在⊙P上或其外部,
∴R≤OP,即R≤5 cm.
∴当2.5 cm<R≤5 cm时,射线OM与⊙P有两个公共点.
(1)当射线OM与⊙P相切时,射线OM与⊙P只有一个公共点,过点P作PA⊥OM于A(图略),则在Rt△AOP中,PA = OP·sin 30° = 5×$\frac{1}{2}$ = 2.5(cm).
∴当R = 2.5 cm时,射线OM与⊙P只有一个公共点.
当射线OM与⊙P相交时,则必须R>2.5 cm.
又
∵点O在⊙P内,
∴R>OP,即R>5 cm.
∴当R = 2.5 cm或R>5 cm时,射线OM与⊙P只有一个公共点.
(2)当射线OM与⊙P相交时,则必须R>2.5 cm.
又
∵点O在⊙P上或其外部,
∴R≤OP,即R≤5 cm.
∴当2.5 cm<R≤5 cm时,射线OM与⊙P有两个公共点.
查看更多完整答案,请扫码查看


