《2025年考点集训与满分备考九年级数学全一册下人教版》

24. (10分)[山东青岛期末]如图，为了测量某大厦AB的高度，某数学实践小组在D处测得楼顶B的仰角为22°，仪器CD的高度为2 m，将仪器CD沿着CA方向前进735 m到达EF，在F处测得楼顶B的仰角为37°，请计算该大厦AB的高度.
参考数据：sin22°≈$\frac{3}{8}$，tan22°≈$\frac{2}{5}$，cos37°≈$\frac{4}{5}$，tan37°≈$\frac{3}{4}$

答案：
[解析]如图，连接DF并延长，交AB于点G，则四边形CDFE和四边形EFGA是矩形，EF = CD = GA，DF = CE，FG = AE，由题意，知CE = 735 m，CD = EF = AG = 2 m，∠BDG = 22°，∠BFG = 37°，在△BGF中，
∵$\tan\angle BFG=\frac{BG}{FG}$，
∴BG = FG·$\tan37^{\circ}$，在△BDG中，$\tan\angle BDG=\frac{BG}{DG}$，
∴BG = DG·$\tan22^{\circ}=(DF + FG)·$\tan22^{\circ}=(735 + FG)·$\tan22^{\circ}$，
∴FG·$\tan37^{\circ}=(735 + FG)·$\tan22^{\circ}$，∴FG≈840 m，∴BG = FG·$\tan37^{\circ}\approx630$m，
∴AB = BG + AG = 630 + 2 = 632(m)，
∴该大厦AB的高度约是632 m。

25. (12分)[江苏南京玄武区二模]如图，某海域有两个海岛A，B，海岛B位于海岛A的正南方向，这两个海岛之间有暗礁，灯塔C位于海岛A的南偏东47.5°方向上，海岛B的北偏东70°方向上，一艘海轮从海岛B出发，沿正南方向航行32 n mile到达D处，测得灯塔C在北偏东37°方向上.求海岛A，B之间的距离.(参考数据：tan37°≈0.75，tan47.5°≈1.10，tan70°≈2.75)

答案：
[解析]如图，过点C作CE⊥AD于点E.在Rt△DEC中，∠CDE = 37°，
∴$\tan37^{\circ}=\frac{CE}{DE}$，即DE = $\frac{CE}{\tan37^{\circ}}$，在Rt△BCE中，∠CBE = 70°，
∴$\tan70^{\circ}=\frac{CE}{BE}$，即BE = $\frac{CE}{\tan70^{\circ}}$，
∵BD = DE - BE，
∴$\frac{CE}{\tan37^{\circ}}-\frac{CE}{\tan70^{\circ}} = 32$，解得CE≈33 n mile，
∴BE = $\frac{CE}{\tan70^{\circ}}\approx\frac{33}{2.75}=12$n mile，在Rt△ACE中，∠CAE = 47.5°，
∴$\tan47.5^{\circ}=\frac{CE}{AE}$，即AE = $\frac{CE}{\tan47.5^{\circ}}\approx30$n mile，
∴AB = AE + BE = 30 + 12 = 42(n mile)，即海岛A，B之间的距离约为42 n mile。

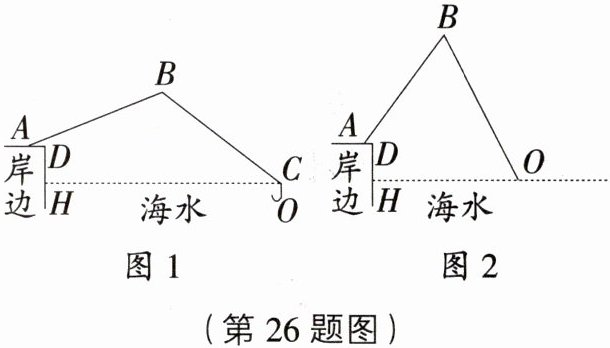
26. (12分)[浙江舟山二模]小明的爸爸周末去某海岛钓鱼，将鱼竿AB摆成如图1所示.已知AB=4.8 m，鱼竿尾端A离岸边0.4 m，即AD=0.4 m.海面与地面AD平行且相距1.2 m，即DH=1.2 m.
(1)如图1，在无鱼上钩时，海面上方的鱼线BC与海面HC的夹角∠BCH=37°，海面下方的鱼线CO与海面HC垂直，鱼竿AB与地面AD的夹角∠BAD=22°.求点O到岸边DH的距离；
(2)如图2，在有鱼上钩时，鱼竿与地面的夹角∠BAD=53°，此时鱼线被拉直，鱼线BO=5.46 m，点O恰好位于海面.求点O到岸边DH的距离.
参考数据：sin37°=cos53°≈$\frac{3}{5}$，cos37°=sin53°≈$\frac{4}{5}$，tan37°≈$\frac{3}{4}$，sin22°≈$\frac{3}{8}$，cos22°≈$\frac{15}{16}$，tan22°≈$\frac{2}{5}$

答案：
［解析］
(1)如图1，过点B作BF⊥CH,垂足为F,延长AD交BF于点E,则四边形DHFE为矩形，AE⊥BF,.. cos ∠BAE= $\frac{AE}{AB}$ ,.. cos 22°= $\frac{AE}{4.8}$ ,
∴ $\frac{15}{16}$ ≈ $\frac{AE}{4.8}$ ,即AE≈4.5m,..DE=AE−AD=4.5−0.4=4.1(m),.. s in ∠BAE= $\frac{BE}{AB}$ ,.. sin 22°= $\frac{BE}{4.8}$ ,
∴ $\frac{3}{8}$ $\frac{BE}{4.8}$ ,即BE≈1.8m,..BF=BE+EF=1.8+1.2=3(m),又 tan ∠BCF= $\frac{BF}{CF}$ ,
∴ tan 37°= $\frac{BF}{CF}$ CF≈4m,
∴ CH=CF+HF=CF+DE=4+4.1=8.1(m),即点0到岸边DH的距离约为8.1m;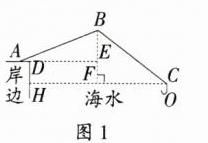
(2)如图2,过点B作BN⊥OH,垂足为点N,延长AD交BN于点M,则四边形DHNM为矩形，..AM⊥BN,
∵ Cos∠BAM= $\frac{AM}{AB}$ ,.. cos 53°= $\frac{AM}{4.8}$ ..
∴ $\frac{3}{5}$  $\frac{AM}{4.8}$ ,即AM≈2.88m,..DM=AM−AD=2.88−0.4=2.48(m),由 s in ∠BAM= $\frac{BM}{AB}$ ,.. s in 53°= $\frac{BM}{4.8}$ ..
∴ $\frac{4}{5}$ $\frac{BM}{4.8}$ ,即BM~3.84m,..BN=BM+MN=3.84+1.2=5.04(m),..ON= $\sqrt{OB−BN2}$ = $\sqrt{5.462−5.042}$ =$\sqrt{4.41}$ =2.1(m),
∴ OH=ON+HN=ON+DM≈4.58(m),即点0到岸边DH的距离约为4.58m.