《2025年考点集训与满分备考九年级数学全一册下人教版》

1. 已知$y = 2x^{2m}$是反比例函数，则$m$的值是 ( )
A. $m=\frac{1}{2}$
B. $m = -\frac{1}{2}$
C. $m\neq0$
D. 一切实数

答案： B ［解析］因为$y = 2x^{2m}$是反比例函数，所以$2m=-1$，所以$m =-\frac{1}{2}$．

2. 已知线段$a = 2$，$b = 3$，$c = 4$，则下列给出的线段$d$的长度能与$a$，$b$，$c$构成比例线段的是 ( )
A. 3
B. 4
C. 5
D. 6

答案： D ［解析］A.$2×4≠3×3$，故线段$d$的长度不能与$a$，$b$，$c$构成比例线段；B.$4×2≠3×4$，故线段$d$的长度不能与$a$，$b$，$c$构成比例线段；C.$5×2≠3×4$，故线段$d$的长度不能与$a$，$b$，$c$构成比例线段；D.$2×6 = 3×4$，故线段$d$的长度能与$a$，$b$，$c$构成比例线段．

3. 在下列四个命题中：①所有等腰直角三角形都相似；②所有等边三角形都相似；③所有正方形都相似；④所有菱形都相似.其中真命题有 ( )
A. 4个
B. 3个
C. 2个
D. 1个

答案： B ［解析］①②③中，各组图形角分别相等，对应边成比例，故正确；④中，所有菱形的四个角不一定相等，因此不都相似，故错误．

4. 姜老师给出一个函数解析式，甲、乙、丙三位同学分别正确指出了这个函数的一个性质.甲：函数图象经过第一象限；乙：函数图象经过第三象限；丙：在每一个象限内，$y$值随$x$值的增大而减小.根据他们的描述，姜老师给出的这个函数解析式可能是 ( )
A. $y = 3x$
B. $y=\frac{3}{x}$
C. $y = -\frac{1}{x}$
D. $y = x^{2}$

答案： B ［解析］$y = 3x$的图象是经过第一、三象限过原点的直线，$y$随$x$的增大而增大，故选项A错误；$y=\frac{3}{x}$的图象在第一、三象限，在每一个象限内$y$随$x$的增大而减小，故选项B正确；$y =-\frac{1}{x}$的图象在第二、四象限，故选项C错误；$y = x^{2}$的图象在第一、二象限，故选项D错误．

5. 如图，$AB$与$CD$相交于点$E$，点$F$在线段$BC$上，且$AC// EF// DB$.若$BE = 5$，$BF = 3$，$AE = BC$，则$\frac{BD}{AC}$的值为 ( )

A. $\frac{2}{3}$
B. $\frac{1}{2}$
C. $\frac{3}{5}$
D. $\frac{2}{5}$

答案： A ［解析］设$CF = x$，$\because EF// AC$，$\therefore\frac{BF}{CF}=\frac{BE}{AE}$，$\therefore\frac{3}{x}=\frac{5}{x + 3}$，解得$x=\frac{9}{2}$，$\therefore CF=\frac{9}{2}$，$\because AC// DB$，$\therefore\triangle ACE\sim\triangle BDE$，$\therefore\frac{BD}{AC}=\frac{BE}{AE}=\frac{5}{3 + \frac{9}{2}}=\frac{2}{3}$．

6. 关于反比例函数$y = -\frac{3}{x}$，下列说法正确的是 ( )
A. 函数图象经过点$(1,3)$
B. 函数图象位于第一、三象限
C. 当$x＞0$时，$y$随$x$的增大而增大
D. 当$1＜x＜3$时，$1＜y＜3$

答案： C ［解析］$\because$函数$y =-\frac{3}{x}$是一个$y$关于$x$的反比例函数，$k=-3\lt0$，$\therefore$函数图象位于第二、四象限，$\because1×3 = 3≠-3$，$\therefore$函数图象不经过点$(1,3)$，根据反比例函数的性质可知，在函数图象的每一个象限内，$y$随$x$的增大而增大，当$1\lt x\lt3$时，$-3\lt y\lt - 1$，$\therefore$说法正确的是当$x\gt0$时，$y$随$x$的增大而增大．

7. 如图，$\triangle ABC\backsim\triangle A'B'C'$，$AD$和$A'D'$分别是$\triangle ABC$和$\triangle A'B'C'$的高，若$AD = 2$，$A'D' = 3$，则$\triangle ABC$与$\triangle A'B'C'$的面积的比为 ( )

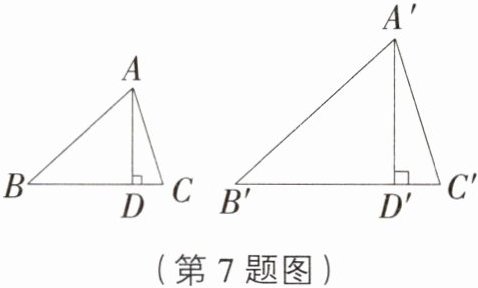
A. 4:9
B. 9:4
C. 2:3
D. 3:2

答案： A ［解析］$\because\triangle ABC\sim\triangle A'B'C'$，$AD$和$A'D'$分别是$\triangle ABC$和$\triangle A'B'C'$的高，$AD = 2$，$A'D' = 3$，$\therefore\frac{AB}{A'B'}=\frac{AD}{A'D'}=\frac{2}{3}$，$\therefore\triangle ABC$与$\triangle A'B'C'$的面积的比$=(\frac{2}{3})^{2}=\frac{4}{9}$．

8. 如图，在$5\times6$的方格纸中，画有格点三角形$EFG$，下列选项中的格点，与$E$，$G$两点构成的三角形中和$\triangle EFG$相似的是 ( )

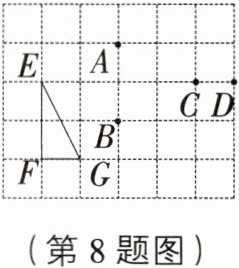
A. 点$A$
B. 点$B$
C. 点$C$
D. 点$D$

答案： D ［解析］观察图形可得$\triangle EFG$中，直角边的比为$\frac{FG}{EF}=\frac{1}{2}$，观察各选项，$\frac{EG}{DG}=\frac{\sqrt{5}}{2\sqrt{5}}=\frac{1}{2}$，只有D选项符合．

9. 已知点$A(x_{1},y_{1})$，$B(x_{2},y_{2})$，$C(x_{3},y_{3})$都在反比例函数$y=\frac{a^{2}+1}{x}$($a$是常数)的图象上，且$y_{1}＜y_{2}＜0＜y_{3}$，则$x_{1}$，$x_{2}$，$x_{3}$的大小关系为 ( )
A. $x_{2}＞x_{1}＞x_{3}$
B. $x_{1}＞x_{2}＞x_{3}$
C. $x_{3}＞x_{2}＞x_{1}$
D. $x_{3}＞x_{1}＞x_{2}$

答案：
D ［解析］$\because a^{2}+1\gt0$，$\therefore$反比例函数$y=\frac{a^{2}+1}{x}$（$a$是常数）的图象在第一、三象限，如图所示，当$y_{1}\lt y_{2}\lt0\lt y_{3}$时，则$x_{3}\gt0\gt x_{1}\gt x_{2}$．

10. 在直角坐标系中，反比例函数$y=\frac{3}{x}(x＞0)$与一次函数$y = -x + 4$的图象如图所示，则图中的阴影部分的面积最大的是 ( )

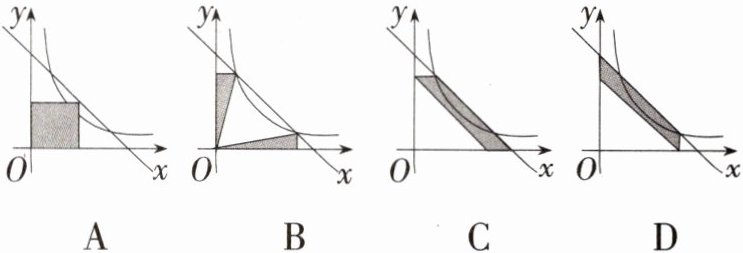
答案： A ［解析］由反比例函数中系数$k$的几何意义可知，选项A中阴影部分的面积大于$3$，选项B，C，D中的阴影部分的面积都等于$3$．