《2025年考点集训与满分备考九年级数学全一册下人教版》

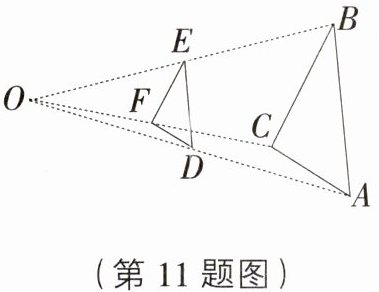
11. 如图，在$\triangle ABC$外取一点$O$，连接$AO$，$BO$，$CO$，并分别取它们的中点$D$，$E$，$F$，得到$\triangle DEF$，则下列说法：①$\triangle ABC$与$\triangle DEF$是位似图形；②$\triangle ABC$与$\triangle DEF$是相似图形；③$\triangle ABC$与$\triangle DEF$的周长比为$2:1$；④$\triangle ABC$与$\triangle DEF$的面积比为$2:1$，以上说法中正确的个数是 ( )

A. 1
B. 2
C. 3
D. 4

答案： C ［解析］根据位似的定义可得$\triangle ABC$与$\triangle DEF$是位似图形，相似比是$2:1$，则周长的比是$2:1$，因而面积的比是$4:1$，故①②③正确，④错误．

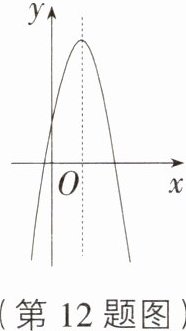
12. 若二次函数$y = ax^{2}+bx + c(a\neq0)$的图象如图所示，则一次函数$y = ax + b$与反比例函数$y = -\frac{c}{x}$在同一个坐标系内的大致图象为 ( )

答案： D ［解析］$\because$抛物线开口向下，对称轴位于$y$轴右侧，与$y$轴的交点在$y$轴正半轴上，$\therefore a\lt0$，$-\frac{b}{2a}\gt0$，$c\gt0$，$\therefore b\gt0$，$\therefore$一次函数$y = ax + b$的图象经过第一、二、四象限，反比例函数$y =-\frac{c}{x}$的图象在第二、四象限．

13. 如图，在平面直角坐标系中，已知点$A(-2,0)$，$B(2,4)$，$C(4,2)$，以点$A$为位似中心，将$\triangle ABC$缩小为$\triangle AB_{1}C_{1}$(同侧)，其相似比为$2:1$，当反比例函数$y=\frac{k}{x}(k\neq0)$的图象经过$B_{1}C_{1}$的中点时，$k$的值为 ( )

A. $\frac{3}{4}$
B. 2
C. -1
D. $\frac{1}{2}$

答案： A ［解析］$\because$点$B$的坐标为$(2,4)$，点$C$的坐标为$(4,2)$，$\therefore BC$的中点坐标为$(3,3)$，以点$A$为原点、原$x$轴为$x$轴建立新的坐标系，则$BC$的中点在新坐标系中的坐标为$(5,3)$，$\because$以点$A$为位似中心，将$\triangle ABC$缩小为$\triangle AB_{1}C_{1}$（同侧），相似比为$2:1$，$\therefore B_{1}C_{1}$的中点在新坐标系中的坐标为$(5\times\frac{1}{2},3\times\frac{1}{2})$，即$(\frac{5}{2},\frac{3}{2})$，则$B_{1}C_{1}$的中点在原坐标系中的坐标为$(\frac{1}{2},\frac{3}{2})$，$\because$反比例函数$y=\frac{k}{x}$（$k\neq0$）的图象经过$B_{1}C_{1}$的中点，$\therefore k=\frac{1}{2}\times\frac{3}{2}=\frac{3}{4}$．

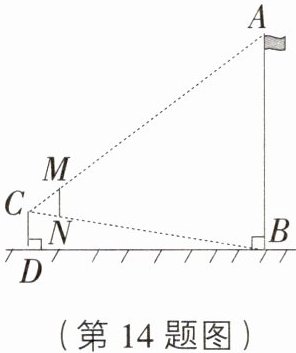
14. 如图，小明到操场测量旗杆$AB$的高度，他手拿一支铅笔$MN$，边观察边移动(铅笔$MN$始终与地面垂直).当小明移动到$D$点时，眼睛$C$与铅笔顶端$M$，旗杆的顶端$A$共线，同时眼睛$C$与它们的底端$N$，$B$也恰好共线.此时测得$DB = 50\ m$，小明的眼睛$C$到铅笔的距离为$0.6\ m$，铅笔$MN$的长为$0.16\ m$，则旗杆$AB$的高度为 ( )

A. 15 m
B. $\frac{50}{3}\ m$
C. $\frac{40}{3}\ m$
D. 14 m

答案：
C ［解析］如图，过点$C$作$CF\perp AB$，垂足为点$F$，交$MN$于点$E$．则$CF = DB = 50\ m$，$CE = 0.6\ m$，$\because MN// AB$，$\therefore\triangle CMN\sim\triangle CAB$．$\therefore\frac{CE}{CF}=\frac{MN}{AB}$，$\therefore AB=\frac{MN\cdot CF}{CE}=\frac{0.16\times50}{0.6}=\frac{40}{3}$（$cm$）．

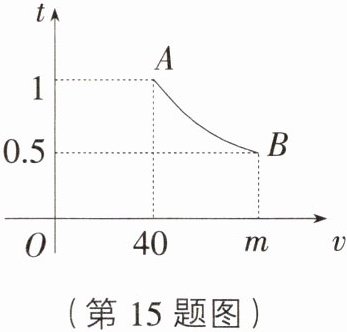
15. 一辆汽车匀速通过某段公路，所需时间$t(\text{h})$与行驶速度$v(\text{km/h})$满足函数关系$t=\frac{k}{v}$，其图象为如图所示的一段曲线，且端点为$A(40,1)$和$B(m,0.5)$，若行驶速度不得超过$60(\text{km/h})$，则汽车通过该路段最少需要时间为 ( )

A. $\frac{2}{3}\ \text{min}$
B. 40 min
C. 60 min
D. $\frac{200}{3}\ \text{min}$

答案： B ［解析］由题意，函数图象经过点$(40,1)$，把$(40,1)$代入$t=\frac{k}{v}$，得$k = 40$，则解析式为$t=\frac{40}{v}$，再把$(m,0.5)$代入$t=\frac{40}{v}$，得$m = 80$；把$v = 60$代入$t=\frac{40}{v}$，得$t=\frac{2}{3}$，$\frac{2}{3}\ h = 40\ min$．

16. 如图，正比例函数$y_{1}=mx$，一次函数$y_{2}=ax + b$和反比例函数$y_{3}=\frac{k}{x}$的图象在同一平面直角坐标系中，若$y_{3}＞y_{2}＞y_{1}$，则自变量$x$的取值范围是 ( )

A. $x＜-1$
B. $-1＜x＜0$或$x＞1.6$
C. $-1＜x＜0$
D. $x＜-1$或$0＜x＜1$

答案： B ［解析］由图象可知，当$-1\lt x\lt0$或$x\gt1.6$时，双曲线$y_{3}$落在直线$y_{2}$上方，且直线$y_{2}$落在直线$y_{1}$上方，即$y_{3}\gt y_{2}\gt y_{1}$，所以若$y_{3}\gt y_{2}\gt y_{1}$，则自变量$x$的取值范围是$-1\lt x\lt0$或$x\gt1.6$．