第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
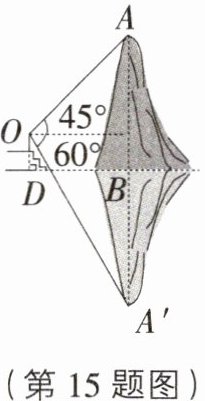
15. [陕西中考]小宸想利用测量知识测算湖中小山的高度.他站在湖边看台上,清晰地看到小山倒映在平静的湖水中,如图所示,他在点O处测得小山顶端的仰角为45°,小山顶端A在水中倒影A'的俯角为60°.已知:点O到湖面的距离OD=3 m,OD⊥DB,AB⊥DB,A,B,A'三点共线,A'B=AB,求小山的高度AB.(光线的折射忽略不计;结果保留根号)

答案:
[解析]如图,过点O作OE⊥AB于点E,则BE = OD = 3 m,设AE = x m,则AB = (x + 3) m,A'E = (x + 6) m,
∵∠AOE = 45°,
∴OE = AE = x m,
∵∠A'OE = 60°,
∴tan60° = $\frac{A'E}{OE}$ = $\sqrt{3}$,即$\frac{x + 6}{x}$ = $\sqrt{3}$,解得x = $3 + 3\sqrt{3}$,
∴AE = $(3 + 3\sqrt{3})$ m,
∴AB = AE + BE = $(6 + 3\sqrt{3})$ m.

[解析]如图,过点O作OE⊥AB于点E,则BE = OD = 3 m,设AE = x m,则AB = (x + 3) m,A'E = (x + 6) m,
∵∠AOE = 45°,
∴OE = AE = x m,
∵∠A'OE = 60°,
∴tan60° = $\frac{A'E}{OE}$ = $\sqrt{3}$,即$\frac{x + 6}{x}$ = $\sqrt{3}$,解得x = $3 + 3\sqrt{3}$,
∴AE = $(3 + 3\sqrt{3})$ m,
∴AB = AE + BE = $(6 + 3\sqrt{3})$ m.

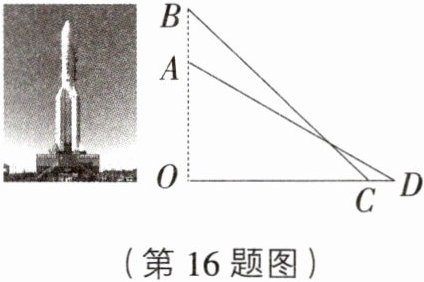
16. [山东枣庄中考]如图,运载火箭从地面O处发射,当火箭到达点A时,地面D处的雷达站测得AD=4 000 m,仰角为30°,3 s后,火箭直线上升到点B处,此时地面C处的雷达站测得B处的仰角为45°.O,C,D在同一直线上,已知C,D两处相距460 m,求火箭从A到B处的平均速度.(结果保留整数,参考数据:$\sqrt{3}\approx1.732$,$\sqrt{2}\approx1.414$)

答案:
[解析]由题意,得AD = 4000 m,∠ADO = 30°,CD = 460 m,∠BCO = 45°,在Rt△AOD中,
∵AD = 4000 m,∠ADO = 30°,
∴OA = $\frac{1}{2}$AD = 2000 m,OD = $\frac{\sqrt{3}}{2}$AD = $2000\sqrt{3}$ m,在Rt△BOC中,∠BCO = 45°,
∴OB = OC = OD - CD = $(2000\sqrt{3}-460)$ m,
∴AB = OB - OA = $2000\sqrt{3}-460 - 2000$ ≈ 1004(m),
∴火箭从A到B处的平均速度为1004÷3≈335(m/s),即火箭从A到B处的平均速度约为335 m/s.
∵AD = 4000 m,∠ADO = 30°,
∴OA = $\frac{1}{2}$AD = 2000 m,OD = $\frac{\sqrt{3}}{2}$AD = $2000\sqrt{3}$ m,在Rt△BOC中,∠BCO = 45°,
∴OB = OC = OD - CD = $(2000\sqrt{3}-460)$ m,
∴AB = OB - OA = $2000\sqrt{3}-460 - 2000$ ≈ 1004(m),
∴火箭从A到B处的平均速度为1004÷3≈335(m/s),即火箭从A到B处的平均速度约为335 m/s.
17. [山东滨州三模]关于三角函数有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①
cos(α+β)=cosαcosβ-sinαsinβ②
tan(α+β)=$\frac{\tan\alpha+\tan\beta}{1 - \tan\alpha\cdot\tan\beta}$③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,如:
tan105°=tan(45°+60°)
=$\frac{\tan45°+\tan60°}{1 - \tan45°\cdot\tan60°}=\frac{1+\sqrt{3}}{1 - 1\times\sqrt{3}}$
=$\frac{(1+\sqrt{3})(1+\sqrt{3})}{(1 - \sqrt{3})(1+\sqrt{3})}$
=-(2+$\sqrt{3}$).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
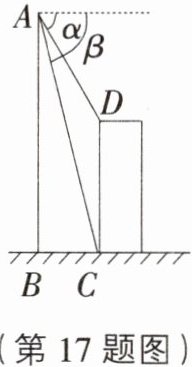
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42 m,求建筑物CD的高.
sin(α+β)=sinαcosβ+cosαsinβ①
cos(α+β)=cosαcosβ-sinαsinβ②
tan(α+β)=$\frac{\tan\alpha+\tan\beta}{1 - \tan\alpha\cdot\tan\beta}$③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,如:
tan105°=tan(45°+60°)
=$\frac{\tan45°+\tan60°}{1 - \tan45°\cdot\tan60°}=\frac{1+\sqrt{3}}{1 - 1\times\sqrt{3}}$
=$\frac{(1+\sqrt{3})(1+\sqrt{3})}{(1 - \sqrt{3})(1+\sqrt{3})}$
=-(2+$\sqrt{3}$).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42 m,求建筑物CD的高.

答案:
[解析]由于α = 60°,β = 75°,BC = 42,则AB = BC·tanβ = 42×tan75° = 42×$\frac{tan45°+tan30°}{1 - tan45°·tan30°}$ = 42×$\frac{1+\frac{\sqrt{3}}{3}}{1-\frac{\sqrt{3}}{3}}$ = $42\sqrt{3}+84$(m),A,D垂直距离为BC·tanα = $42\sqrt{3}$ m,
∴CD = AB - $42\sqrt{3}$ = 84(m).即建筑物CD的高为84 m.
∴CD = AB - $42\sqrt{3}$ = 84(m).即建筑物CD的高为84 m.
查看更多完整答案,请扫码查看


