《2025年考点集训与满分备考九年级数学全一册下人教版》

1. [湖北随州广水期末]如图，在$\triangle ABC$中，$AB = 8$，$AC = 6$，$D$是$AB$的中点.试在$AC$上确定点$E$的位置，使$\triangle ADE$与$\triangle ABC$相似，并求$AE$的长.

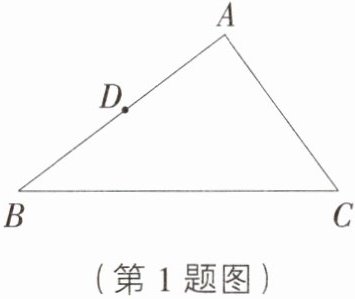
答案：
[解析]
∵D是AB的中点,AB=8,
∴AD=$\frac{1}{2}$AB = 4.
　如图,分两种情况:①作DE₁//BC交AC于E₁,则△ADE₁∽△ABC,
∴$\frac{AD}{AB}=\frac{AE_{1}}{AC}$，即$\frac{4}{8}=\frac{AE_{1}}{6}$，
　解得AE₁ = 3.
　②作∠ADE₂ = ∠C,使DE₂交AC于E₂,
∵∠A = ∠A,当∠ADE₂ = ∠C时,△ADE₂∽△ACB,
∴$\frac{AD}{AC}=\frac{AE_{2}}{AB}$，即$\frac{4}{6}=\frac{AE_{2}}{8}$，
　解得AE₂ = $\frac{16}{3}$，
∴AE的长为3或$\frac{16}{3}$.
　　　

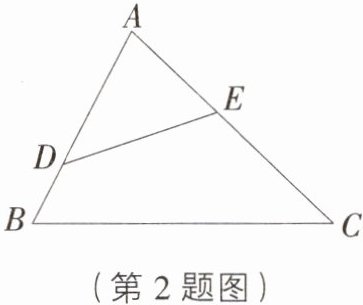
2. [江苏淮安淮阳区模拟]如图，在$\triangle ABC$中，$AB = 6$，$AC = 8$，$D$，$E$分别在$AB$，$AC$上，连接$DE$，设$BD = x(0 ＜ x ＜ 6)$，$CE = y(0 ＜ y ＜ 8)$.
(1)当$x = 2$，$y = 5$时，求证：$\triangle AED\backsim\triangle ABC$；
(2)若$\triangle ADE$和$\triangle ABC$相似，求$y$与$x$的函数关系式.

答案： [解析]
(1)
∵AB = 6，BD = 2，
∴AD = 4，
∵AC = 8，CE = 5，
∴AE = 3，
∴$\frac{AE}{AB}=\frac{3}{6}=\frac{1}{2}$，$\frac{AD}{AC}=\frac{4}{8}=\frac{1}{2}$，
∴$\frac{AE}{AB}=\frac{AD}{AC}$，
∵∠EAD = ∠BAC，
∴△AED∽△ABC;
(2)①若△ADE∽△ABC,
　则$\frac{6 - x}{6}=\frac{8 - y}{8}$，
∴y = $\frac{4}{3}$x(0 ＜ x ＜ 6);②若△ADE∽△ACB,
　则$\frac{6 - x}{8}=\frac{8 - y}{6}$，
∴y = $\frac{3}{4}$x + $\frac{7}{2}$(0 ＜ x ＜ 6).

3. 如图，在矩形$ABCD$中，$AB = 12\ cm$，$BC = 6\ cm$，点$P$沿边$AB$从点$A$开始向点$B$以$2\ cm/s$的速度移动，点$Q$沿边$DA$从点$D$开始向点$A$以$1\ cm/s$的速度移动，如果$P$，$Q$同时出发，设移动的时间为$t\ s(0\leqslant t\leqslant 6)$.
(1)当$t$为何值时，$QP$的长为$4\sqrt{2}\ cm$?
(2)$t$为何值时，$\triangle QCP$的面积为$27\ cm^{2}$?
(3)是否存在这样的$t$值，使得以点$Q$，$A$，$P$为顶点的三角形与$\triangle ABC$相似？若存在，求出$t$的值；若不存在，说明理由.

答案： [解析]
(1)由题意,得DQ = t cm，AP = 2t cm，∠DAB = 90°，
∴AQ = (6 - t) cm，
∵QP = 4$\sqrt{2}$ cm，根据勾股定理，得(4$\sqrt{2}$)² = (6 - t)² + (2t)²，
　解得t = 2或0.4，
∴当t为2或0.4 时,QP的长为4$\sqrt{2}$ cm;
(2)由S_{△QCP}=S_{矩形 ABCD}-S_{△CDQ}-S_{△AQP}-S_{△BCP}得12×6 - 6t - t(6 - t) - 3(12 - 2t) = 27，解得t₁ = t₂ = 3;
∴t为3时,△QCP的面积为27 cm²;
(3)
∵以点Q,A,P为顶点的三角形与△ABC相似,
　由
(1)得AQ = (6 - t) cm，AP = 2t cm，AB = 12 cm，BC = 6 cm，
　①当△AQP∽△BCA时,则$\frac{AQ}{BC}=\frac{AP}{AB}$，
∴$\frac{6 - t}{6}=\frac{2t}{12}$，解得t = 3;②当△AQP∽△BAC时,则$\frac{AQ}{AB}=\frac{AP}{BC}$，
∴$\frac{6 - t}{12}=\frac{2t}{6}$，解得t = $\frac{6}{5}$，
∴当t = 3或$\frac{6}{5}$时,以点Q,A,P为顶点的三角形与△ABC相似.

4. [浙江绍兴柯桥区八校联考]在平面直角坐标系中，已知矩形$OA_{1}B_{1}C_{1}$与矩形$OABC$关于坐标原点$O$位似，且矩形$OA_{1}B_{1}C_{1}$的面积等于矩形$OABC$面积的$4$倍，若矩形$OABC$的顶点$B$的坐标为$B(8,6)$，则$B$的对应点$B_{1}$的坐标为 （ ）
A. $(8,6)$
B. $(4,3)$或$(-4,-3)$
C. $(16,12)$
D. $(16,12)$或$(-16,-12)$

答案： D　[解析]
∵矩形OA₁B₁C₁与矩形OABC关于坐标原点O位似，且矩形OA₁B₁C₁的面积等于矩形OABC面积的4倍,
∴矩形OA₁B₁C₁与矩形OABC的相似比为2:1,
∵点B的坐标为(8,6)，
∴B的对应点B₁的坐标为(8×2,6×2)或[8×(-2),6×(-2)]，即(16,12)或(-16,-12).