《2025年考点集训与满分备考九年级数学全一册下人教版》

11. [贵州贵阳南明区模拟]如图，在平行四边形$ABCD$中，点$E$在边$DC$上，$DE:EC=3:1$，连接$AE$交$BD$于点$F$，则$\triangle DEF$的面积与$\triangle DAF$的面积之比为（ ）

A. 9:16
B. 3:4
C. 9:4
D. 3:2

答案： B ［解析］$\because$四边形$ABCD$为平行四边形，$\therefore AB = CD$，$AB// CD$，
$\because DE:EC = 3:1$，$\therefore DE:AB = DE:DC = 3:4$，
$\because DE// AB$，$\therefore\triangle DEF\backsim\triangle BAF$，
$\therefore\frac{EF}{AF}=\frac{DE}{AB}=\frac{3}{4}$，$\because\triangle DEF$与$\triangle DAF$同高，$\therefore\triangle DEF$的面积与$\triangle DAF$的面积之比$=EF:AF = 3:4$.

12. 易错[山东菏泽巨野期中]已知$\triangle ABC\backsim\triangle DEF$，且$\triangle ABC$与$\triangle DEF$的面积比为9:4，$\triangle ABC$的最短边长为6 cm，则$\triangle DEF$的最短边长为 ______.

答案： $4\ cm$ ［解析］设$\triangle DEF$的最短边边长是$x\ cm$，$\because\triangle ABC\backsim\triangle DEF$，面积比为$9:4$，$\therefore\triangle ABC$与$\triangle DEF$的对应边之比为$3:2$.$\therefore 6:x = 3:2$.则$x = 4$.

13. [河北石家庄辛集期中]已知两相似三角形对应角平分线的比为3:10，且大三角形的面积为400 $cm^{2}$，求小三角形的面积.

答案： ［解析］设小三角形的面积为$S\ cm^{2}$，
$\because$两相似三角形对应角平分线的比为$3:10$，$\therefore$两相似三角形的相似比为$3:10$，$\therefore\frac{S}{400}=(\frac{3}{10})^{2}=\frac{9}{100}$，$\therefore S = 36$，即小三角形的面积为$36\ cm^{2}$.

14. [浙江杭州大关中学月考]如图，在四边形$ABCD$中，$E$是$AD$上的一点，$EC// AB$，$EB// DC$.
(1)$\triangle ABE$与$\triangle ECD$相似吗？为什么？
(2)设$\triangle ABE$的边$BE$上的高为$h_{1}$，$\triangle ECD$的边$CD$上的高为$h_{2}$，$\triangle ABE$的面积为3，$\triangle ECD$的面积为1.
①求$\frac{h_{1}}{h_{2}}$的值；
②求$\triangle BCE$的面积.

答案：
［解析］（1）$\triangle ABE$与$\triangle ECD$相似.
理由：$\because EC// AB$，$\therefore\angle A=\angle CED$，
$\because EB// DC$，$\therefore\angle AEB=\angle D$，
$\therefore\triangle ABE\backsim\triangle ECD$；
（2）①由（1）得$\triangle ABE\backsim\triangle ECD$，
$\therefore(\frac{h_{1}}{h_{2}})^{2}=\frac{3}{1}$，$\therefore\frac{h_{1}}{h_{2}}=\sqrt{3}$（负值已舍去）；
②如图，过点$E$作$EM\perp CD$于点$M$，过点$C$作$CN\perp BE$于点$N$，$\because EB// DC$，$\therefore EM = CN$，
$\because\triangle ABE\backsim\triangle ECD$，$\triangle ABE$的面积为$3$，$\triangle ECD$的面积为$1$，
$\therefore(\frac{BE}{CD})^{2}=\frac{3}{1}$，$\therefore\frac{BE}{CD}=\sqrt{3}$（负值舍去），即$BE=\sqrt{3}CD$，
$\therefore\frac{S_{\triangle BCE}}{S_{\triangle ECD}}=\frac{\frac{1}{2}BE\cdot CN}{\frac{1}{2}CD\cdot EM}=\frac{BE}{CD}=\sqrt{3}$，
$\therefore\frac{S_{\triangle BCE}}{1}=\sqrt{3}$，$\therefore S_{\triangle BCE}=\sqrt{3}$.

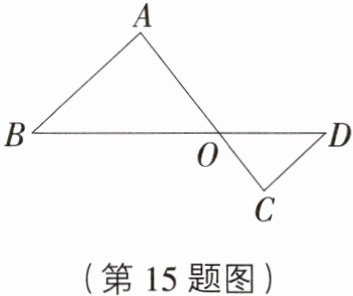
15. [重庆中考]如图，$\triangle ABO\backsim\triangle CDO$，若$BO=6$，$DO=3$，$CD=2$，则$AB$的长是（ ）


A. 2
B. 3
C. 4
D. 5

答案： C ［解析］$\because\triangle ABO\backsim\triangle CDO$，
$\therefore\frac{BO}{DO}=\frac{AB}{DC}$，$\because BO = 6$，$DO = 3$，$CD = 2$，
$\therefore\frac{6}{3}=\frac{AB}{2}$，解得$AB = 4$.

16. [江苏镇江中考]如图，点$D$，$E$分别在$\triangle ABC$的边$AC$，$AB$上，$\triangle ADE\backsim\triangle ABC$，$M$，$N$分别是$DE$，$BC$的中点，若$\frac{AM}{AN}=\frac{1}{2}$，则$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=$ ______.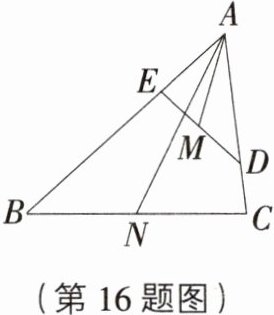

答案： $\frac{1}{4}$ ［解析］$\because M$，$N$分别是$DE$，$BC$的中点，$\therefore AM$，$AN$分别为$\triangle ADE$，$\triangle ABC$的中线，$\because\triangle ADE\backsim\triangle ABC$，
$\therefore\frac{DE}{BC}=\frac{AM}{AN}=\frac{1}{2}$，
$\therefore\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=(\frac{DE}{BC})^{2}=\frac{1}{4}$.

17. [河北保定莲池区期中]如图，小明作出了边长为1的第1个等边三角形$A_{1}B_{1}C_{1}$，算出了等边三角形$A_{1}B_{1}C_{1}$的面积，然后分别取$\triangle A_{1}B_{1}C_{1}$三边的中点$A_{2}$，$B_{2}$，$C_{2}$，作出了第2个等边三角形$A_{2}B_{2}C_{2}$，算出了等边三角形$A_{2}B_{2}C_{2}$的面积.用同样的方法，作出了第3个等边三角形$A_{3}B_{3}C_{3}$，算出了等边三角形$A_{3}B_{3}C_{3}$的面积……由此可得，第10个等边三角形$A_{10}B_{10}C_{10}$的面积是（ ）
A. $\frac{\sqrt{3}}{4}\times(\frac{1}{4})^{9}$
B. $\frac{\sqrt{3}}{4}\times(\frac{1}{4})^{10}$
C. $\frac{\sqrt{3}}{4}\times(\frac{1}{2})^{9}$
D. $\frac{\sqrt{3}}{4}\times(\frac{1}{2})^{10}$

答案： A ［解析］因为等边三角形$A_{1}B_{1}C_{1}$的面积是$\frac{\sqrt{3}}{4}$，而$\triangle A_{2}B_{2}C_{2}$与$\triangle A_{1}B_{1}C_{1}$相似，并且相似比是$1:2$，则面积的比是$\frac{1}{4}$，则等边三角形$A_{2}B_{2}C_{2}$的面积是$\frac{\sqrt{3}}{4}\times\frac{1}{4}$，因而等边三角形$A_{3}B_{3}C_{3}$与等边三角形$A_{2}B_{2}C_{2}$的面积的比也是$\frac{1}{4}$，故$\triangle A_{3}B_{3}C_{3}$的面积是$\frac{\sqrt{3}}{4}\times(\frac{1}{4})^{2}$；依此类推，$\triangle A_{n}B_{n}C_{n}$与$\triangle A_{n - 1}B_{n - 1}C_{n - 1}$的面积的比是$\frac{1}{4}$，第$n$个三角形的面积是$\frac{\sqrt{3}}{4}\times(\frac{1}{4})^{n - 1}$，所以第$10$个等边三角形$A_{10}B_{10}C_{10}$的面积是$\frac{\sqrt{3}}{4}\times(\frac{1}{4})^{9}$.