《2025年考点集训与满分备考九年级数学全一册下人教版》

14. [云南模拟]已知某品牌显示器的使用寿命为定值.这种显示器可工作的天数y与平均每天工作的小时数x是反比例函数关系，图象如图所示.如果这种显示器至少要用2 000天，那么显示器平均每天工作的小时数x应控制在 （ ）

A. 0＜x≤10
B. 10≤x≤24
C. 0＜x≤20
D. 20≤x≤24

答案： 14.A　[解析]由题意可设y=$\frac{k}{x}$(k≠0),
∵图象过点(20,1000),
　..k=20000...y=$\frac{20000}{x}$(x＞0).
∴当y=2000时，x=10.观察图象，可得当y≥2000时,0＜x≤10.

15. 重点[河南安阳模拟]已知蓄电池的电压为定值，使用电池时，电流I(A)与电阻R(Ω)是反比例函数关系，图象如图所示，如果以此蓄电池为电源的电器的限制电流不能超过b A，那么电器的可变电阻R(Ω)应控制在（ ）

A. R≥0
B. R≥a
C. 0＜R≤a
D. 0＜R≤b

答案： 15.B　　[解析]设反比例函数关系式为1=$\frac{k}{R}$,把(a,b)代入,得k=ab,
∴反比例函数关系式为=$\frac{ab}{R}$,当1≤b时,$\frac{ab}{R}$≤b,..R≥a.

16. [河北保定定兴模拟]琪琪同学训练某种运算技能，每次训练完成相同数量的题目，各次训练题目难度相当.当训练次数不超过15次时，完成一次训练所需要的时间y(单位：s)与训练次数x(单位：次)之间满足如图所示的反比例函数关系.完成第3次训练所需时间为400 s.
(1)y与x之间的函数关系式为________，x的取值范围是______；
(2)当x的值为6，8，10时，对应的函数值分别为y1，y2，y3，比较(y1 - y2)与(y2 - y3)的大小：y1 - y2__________y2 - y3.

答案： 16.
(1)y=$\frac{1200}{x}$　0＜x≤15　
(2)＞
[解析]
(1)设y与x之间的函数关系式为y=$\frac{k}{x}$(k≠0,0＜x≤15),把(3,400)
代入y=$\frac{k}{x}$得,400=$\frac{k}{3}$,解得k=
　1200.y与x之间的函数关系式为y=$\frac{1200}{x}$,x的取值范围是0＜x≤15;
(2)把x=6,8,10分别代入y=$\frac{1200}{x}$
　得y=$\frac{1200}{6}$=200,y2=$\frac{1200}{8}$=150,y=$\frac{1200}{10}$=120，y1−y2=200−150=
　50,y2−y3=150−120=30,
∵50＞30,...y1−y2＞y2−y3.

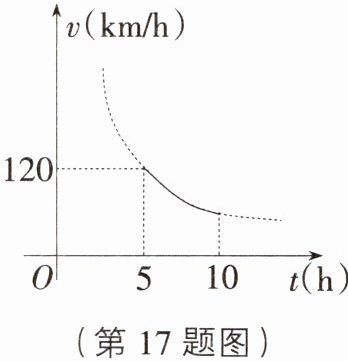
17. [河北模拟]一辆客车从甲地出发前往乙地，平均速度v(km/h)与所用时间t(h)的函数关系如图所示，其中60≤v≤120.
(1)求v与t的函数关系式及t值的取值范围；
(2)客车上午8时从甲地出发.
①客车需在当天14时40分至15时30分(含14时40分与15时30分)间到达乙地，求客车行驶速度v的范围；
②客车能否在当天12时30分前到达乙地？说明理由.

答案： 17.[解析]
(1)设v与t的函数关系式为=$\frac{k}{t}$,将(5,120)代入v=$\frac{k}{t}$,得120=$\frac{k}{5}$,解得k=600，与t的函数关系式为v=$\frac{600}{t}$(5≤t≤10);
(2)①当t=$\frac{20}{3}$(8时到14时40分)
　时,v=$\frac{600}{t}$=600÷$\frac{20}{3}$=90(km/h),当=$\frac{15}{2}$(8时到15时30分)时,v=
　$\frac{600}{t}$=600÷$\frac{15}{2}$=80(km/h),
∴客车行驶速度的范围为80km/h≤u≤90km/h;
　②不能.理由:当天12时30分到达时,t=4.5＜5,而5≤t≤10,故客车不能在当天12时30分前到达乙地.能在当天12时30分前到达乙地.

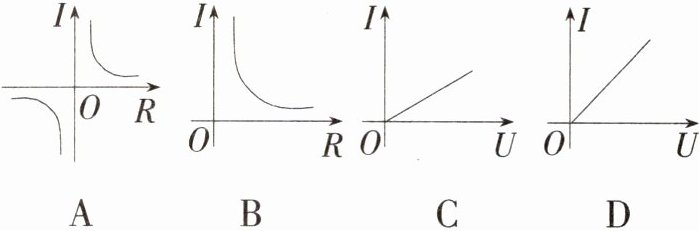
18. [湖北宜昌中考]已知电压U、电流I、电阻R三者之间的关系式为U=IR(或者$I=\frac{U}{R}$)，实际生活中，由于给定已知量不同，因此会有不同的可能图象，图象不可能是 （ ）

答案： 18.A　[解析]当U一定时,电压U、电流I、电阻R三者之间的关系式为1=$\frac{U}{R}$,1与R成反比例函数关系,但R不能小于0,所以图象A不可能，
B可能;当R一定时,电压U、电流1、电阻R三者之间的关系式为U=
　IR,U和I成正比例函数关系，所以
C,D均有可能,