《2025年考点集训与满分备考九年级数学全一册下人教版》

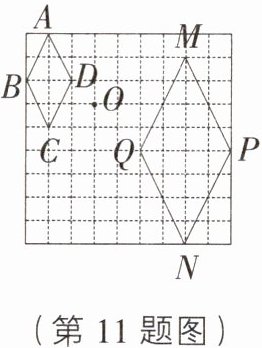
11. 在如图所示的网格中，四边形ABCD的位似图形是四边形NPMQ，位似中心是点O，则四边形ABCD与四边形NPMQ的相似比是( )

A. 1:2
B. 2:1
C. 1:$\sqrt{2}$
D. $\sqrt{2}$:1

答案：
A [解析] 如图，连接 $OD$，$OQ$，$\because$ 四边形 $ABCD$ 的位似图形是四边形 $NPMQ$，位似中心是点 $O$，$\therefore$ 四边形 $ABCD$ 与四边形 $NPMQ$ 的相似比 $=OD:OQ=\sqrt{2}:2\sqrt{2}=1:2$。

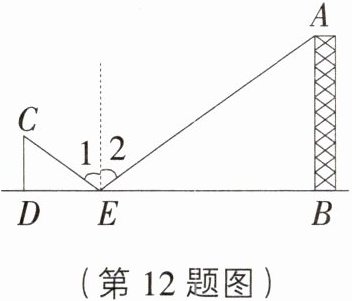
12. 如图，某数学活动小组为测量校园内移动信号转播塔AB的高度，他们先在水平地面上一点E放置了一个平面镜，镜子与铁塔底端B的距离BE=16 m，当镜子与观测者小芳的距离ED=2 m时，小芳刚好从镜子中看到移动信号转播塔的顶端A，已知小芳的眼睛距地面的高度CD=1.5 m，移动信号转播塔AB的高度为(根据光的反射原理，∠1=∠2)( )

A. 9 m
B. 12 m
C. 15 m
D. 18 m

答案： B [解析] 由题意知 $\triangle CDE\sim\triangle ABE$，$\therefore\frac{DE}{BE}=\frac{CD}{AB}$，$\therefore\frac{2}{16}=\frac{1.5}{AB}$，$\therefore AB = 12\ m$。

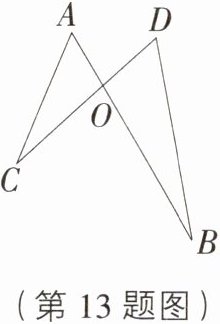
13. 如图所示，AB，CD相交于点O，连接AC，BD，添加下列一个条件后，仍不能判定△AOC∽△DOB的是( )

A. ∠A=∠D
B. $\frac{AO}{OD}=\frac{OC}{OB}$
C. ∠B=∠C
D. $\frac{AC}{BD}=\frac{AO}{OD}$

答案： D [解析] 由图可得 $\angle AOC=\angle BOD$，所以要使 $\triangle AOC\sim\triangle DOB$ 只需再添加一个对应角相等或已知等角为夹角的两对应边成比例即可，所以题中选项 A，B，C 均符合题意，而 D 选项中 $AC$ 与 $AO$ 的夹角并不是 $\angle AOC$，所以其不能判定两个三角形相似。

14. 在平面直角坐标系中，△ABC和△A₁B₁C₁的相似比等于$\frac{1}{2}$，并且是关于原点O的位似图形，若点A的坐标为(2,4)，则其对应点A₁的坐标是( )
A. (4,8)
B. (-1,-2)
C. (1,2)或(-1,-2)
D. (4,8)或(-4,-8)

答案： D [解析] $\because\triangle ABC$ 和 $\triangle A_1B_1C_1$ 是关于原点 $O$ 的位似图形，相似比等于 $\frac{1}{2}$，点 $A$ 的坐标为 $(2,4)$，$\therefore$ 点 $A_1$ 的坐标为 $(4,8)$ 或 $(-4,-8)$。

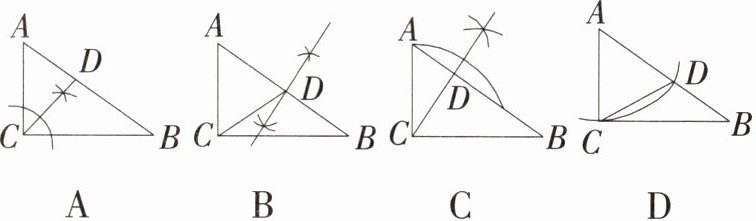
15. 在△ABC中，∠ACB=90°，用直尺和圆规在AB上确定点D，使△ACD∽△CBD，根据作图痕迹判断，正确的是( )

答案： C [解析] 当 $CD$ 是 $AB$ 的垂线时，$\triangle ACD\sim\triangle CBD$。$\because CD\perp AB$，$\therefore\angle CDA=\angle BDC = 90^{\circ}$，$\because\angle ACB = 90^{\circ}$，$\therefore\angle A+\angle ACD=\angle ACD+\angle BCD = 90^{\circ}$，$\therefore\angle A=\angle BCD$，$\therefore\triangle ACD\sim\triangle CBD$。根据作图痕迹可知，A 选项中，$CD$ 是 $\angle ACB$ 的平分线，不符合题意；B 选项中，$CD$ 不与 $AB$ 垂直，不符合题意；C 选项中，$CD$ 是 $AB$ 的垂线，符合题意；D 选项中，$CD$ 不与 $AB$ 垂直，不符合题意。

16. 如图，在钝角三角形ABC中，AB=6 cm，AC=12 cm，动点D从点A出发沿AB以1 cm/s的速度向点B运动，同时动点E从点C出发沿CA以2 cm/s的速度向点A运动，当以A，D，E为顶点的三角形与△ABC相似时，运动时间是( )

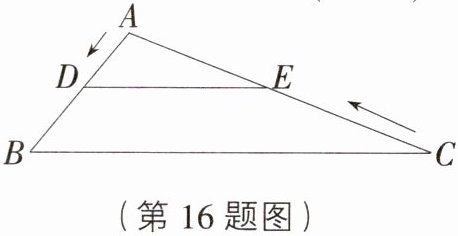
A. 3 s或4.8 s
B. 3 s
C. 4.5 s
D. 4.5 s或4.8 s

答案： A [解析] 两点同时运动，设运动 $t\ s$ 时，以点 $A$，$D$，$E$ 为顶点的三角形与 $\triangle ABC$ 相似，则 $AD = t\ cm$，$CE = 2t\ cm$，$AE=(12 - 2t)\ cm$，
①当 $D$ 与 $B$ 对应时，有 $\triangle ADE\sim\triangle ABC$，$\therefore AD:AB = AE:AC$，$\therefore t:6=(12 - 2t):12$，$\therefore t = 3$；
②当 $D$ 与 $C$ 对应时，有 $\triangle ADE\sim\triangle ACB$，$\therefore AD:AC = AE:AB$，$\therefore t:12=(12 - 2t):6$，$\therefore t = 4.8$，$\therefore$ 当以点 $A$，$D$，$E$ 为顶点的三角形与 $\triangle ABC$ 相似时，运动时间是 $3\ s$ 或 $4.8\ s$。

17. 如图，△ABC与△DEF是位似图形，位似中心为O，OA:AD=3:4，S△ABC=9，则△DEF的面积为________.

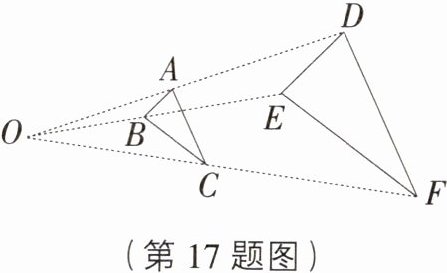
答案： 49 [解析] $\because OA:AD = 3:4$，$\therefore OA:OD = 3:7$，$\because\triangle ABC$ 与 $\triangle DEF$ 是位似图形，$\therefore AB// DE$，$\therefore\triangle OAB\sim\triangle ODE$，$\therefore\frac{AB}{DE}=\frac{OA}{OD}=\frac{3}{7}$，$\therefore\frac{S_{\triangle ABC}}{S_{\triangle DEF}}=(\frac{3}{7})^2=\frac{9}{49}$，$\because S_{\triangle ABC}=9$，$\therefore\triangle DEF$ 的面积为 49。