《2025年考点集训与满分备考九年级数学全一册下人教版》

18. 如图，矩形ABCD中，AB=6，AD=8，点E在边AD上，CE与BD相交于点F.设DE=x，BF=y，当0≤x≤8时，y关于x的函数解析式为____________.

答案： $y=\frac{80}{x + 8}$ [解析] 在矩形 $ABCD$ 中，$AD// BC$，$\therefore\triangle DEF\sim\triangle BCF$，$\therefore\frac{DE}{BC}=\frac{DF}{BF}$，$\because BD=\sqrt{BC^{2}+CD^{2}} = 10$，$BF = y$，$DE = x$，$\therefore DF = 10 - y$，$\therefore\frac{x}{8}=\frac{10 - y}{y}$，化简，得 $y=\frac{80}{x + 8}$。

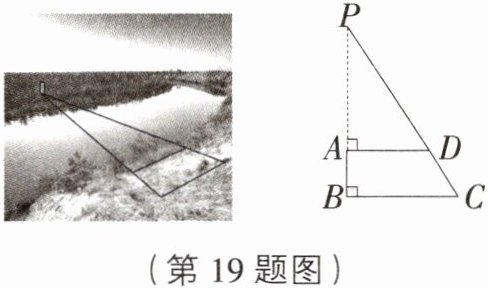
19. 如图，为了确定一条河的宽度，测量人员在对岸岸边P点处观察到一根柱子，再在他们所在的这一侧岸上选点A和点B，使得B，A，P在同一条直线上，且与河岸垂直，随后确定点C，点D，使BC⊥BP，AD⊥BP，由观测可以确定CP与AD的交点D.他们测得AB=45 m，BC=90 m，AD=60 m，从而确定河宽，他们测量的河宽为____________ m.

答案： 90 [解析] $\because BC\perp BP$，$AD\perp BP$，$\therefore AD// BC$，$\therefore\triangle PAD\sim\triangle PBC$，$\therefore\frac{AD}{BC}=\frac{PA}{PB}$，即 $\frac{60}{90}=\frac{PA}{PA + 45}$，解得 $PA = 90\ m$。

20. 如图，△ABC∽△ADE，∠BAC=∠DAE=90°，AB=6，AC=8，点D在线段BC上运动，当点D从点B运动到点C时.
(1)当BD=1时，则CE=______；
(2)设P为线段DE的中点，在点D的运动过程中，CP的最小值是________.

答案：
(1)$\frac{4}{3}$
(2)4
[解析]
(1)$\because\triangle ABC\sim\triangle ADE$，$\therefore\frac{AB}{AD}=\frac{AC}{AE}$，$\angle BAC=\angle DAE$，$\therefore\angle BAD=\angle CAE$，$\frac{AB}{AC}=\frac{AD}{AE}$，$\therefore\triangle BAD\sim\triangle CAE$，$\therefore\frac{BD}{CE}=\frac{AB}{AC}=\frac{6}{8}$，$\because BD = 1$，$\therefore CE=\frac{4}{3}$；
(2)$\because\triangle BAD\sim\triangle CAE$，$\therefore\angle ABD=\angle ACE$，$\because\angle BAC = 90^{\circ}$，$\therefore\angle ABD+\angle ACB = 90^{\circ}$，$\therefore\angle ACB+\angle ACE = 90^{\circ}$，$\therefore\angle DCE = 90^{\circ}$，$\because DP = PE$，$\therefore CP=\frac{1}{2}DE$，$\because\triangle ABC\sim\triangle ADE$，$\therefore$ 当 $AD$ 的值最小时，$DE$ 的值最小，此时 $CP$ 的值最小，$\because AB = 6$，$AC = 8$，$\angle BAC = 90^{\circ}$，$\therefore BC=\sqrt{AB^{2}+AC^{2}}=\sqrt{6^{2}+8^{2}} = 10$，根据垂线段最短可知，当 $AD\perp BC$ 时，$AD$ 的值最小，此时 $AD=\frac{AB\cdot AC}{BC}=\frac{24}{5}$。由 $\triangle ABC\sim\triangle ADE$ 可知 $DE=\frac{5}{3}AD = 8$，$\therefore CP$ 的最小值为 $\frac{1}{2}\times8 = 4$。

21. (6分)[河南部分学校联考]如图，在△ABC中，DF//AC，DE//BC.
(1)求证：$\frac{BF}{FC}=\frac{CE}{EA}$；
(2)若AE=4，EC=2，BC=10，求BF和CF长.

答案： [解析]
(1)$\because DF// AC$，$\therefore\frac{BF}{FC}=\frac{BD}{AD}$，$\because DE// BC$，$\therefore\frac{BD}{AD}=\frac{CE}{EA}$，$\therefore\frac{BF}{FC}=\frac{CE}{EA}$；
(2)设 $BF = x$，$\because BC = 10$，$\therefore CF = 10 - x$，由
(1)得 $\frac{BF}{FC}=\frac{CE}{EA}$，$\because AE = 4$，$EC = 2$，$\therefore\frac{x}{10 - x}=\frac{2}{4}$，$\therefore x=\frac{10}{3}$，$\therefore BF=\frac{10}{3}$，$\therefore CF = 10-\frac{10}{3}=\frac{20}{3}$。

22. (8分)[陕西咸阳寿都区期末]如图，在4×4的正方形网格纸中，△ABC和△DEF的顶点都在边长为1的小正方形的格点上.
(1)求证：△ABC∽△DEF；
(2)直接写出△ABC和△DEF的周长比.

答案： [解析]
(1)$\because AB = 2$，$BC = 2\sqrt{2}$，$AC = 2\sqrt{5}$，$DE=\sqrt{2}$，$EF = 2$，$DF=\sqrt{10}$，$\therefore\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}=\sqrt{2}$，$\therefore\triangle ABC\sim\triangle DEF$；
(2)$\triangle ABC$ 和 $\triangle DEF$ 的周长比 $=\frac{AC}{DF}=\sqrt{2}$。

23. (9分)如图所示的平面直角坐标系中，△ABC的三个顶点坐标分别为A(-3,2)，B(-1,3)，C(-1,1)，请按如下要求画图：
(1)以坐标原点O为旋转中心，将△ABC顺时针旋转90°，得到△A₁B₁C₁，请画出△A₁B₁C₁，并写出点B的对应点B₁的坐标；
(2)以坐标原点O为位似中心，在x轴下方，画出△ABC的位似图形△A₂B₂C₂，使它与△ABC的相似比为2:1，并写出点B的对应点B₂的坐标.
(3)△ABC内部一点M的坐标为(a,b)，写出M在△A₂B₂C₂中的对应点M₂的坐标.

答案：
[解析]
(1)如图，$\triangle A_1B_1C_1$ 即为所求，其中点 $B$ 的对应点 $B_1$ 的坐标为 $(3,1)$；
(2)如图所示，$\triangle A_2B_2C_2$ 即为所求，点 $B$ 的对应点 $B_2$ 的坐标为 $(2,-6)$；
(3)$M$ 在 $\triangle A_2B_2C_2$ 中的对应点 $M_2$ 的坐标为 $(-2a,-2b)$。