《2025年考点集训与满分备考九年级数学全一册下人教版》

13. [河南驻马店平舆期末]如图，在某一时刻小明测得1 m长的竹竿竖直放置时影长为1.2 m，在同一时刻旗杆AB的影长一部分落在水平地面上，另一部分落在楼房的墙上，他测得落在地面上的影长BD=6 m，落在墙上的影长CD=1.4 m，则旗杆的高度为( )

A. 4.8 m
B. 5.2 m
C. 6 m
D. 6.4 m

答案：
D [解析]作CE⊥AB于点E，如图，则四边形BDCE为矩形，BD = CE = 6 m，BE = CD = 1.4 m，根据题意得$\frac{AE}{EC}=\frac{1}{1.2}$，即$\frac{AE}{6}=\frac{1}{1.2}$，解得AE = 5 m，
∴AB = AE + BE = 5 + 1.4 = 6.4(m).

14. [河南许昌长葛模拟]一把剪刀如图所示，AB=2BC，BD=2BE，当手握的地方EC张开3 cm时，剪刀的尖端A，D两点的距离为____ cm.

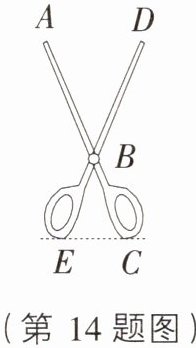
答案： 6 [解析]
∵AB = 2BC，BD = 2BE，
∴$\frac{AB}{BC}=2$，$\frac{BD}{BE}=2$，
∴$\frac{AB}{BC}=\frac{BD}{BE}$，又
∵∠ABD = ∠CBE，
∴△ADB∽△CEB，$\frac{AD}{EC}=\frac{AB}{BC}$，
∴$\frac{AD}{3}=2$，解得AD = 6 cm.

15. [吉林长春德惠期中]如图是小孔成像原理的示意图，根据图中所标注的尺寸，蜡烛AB在暗盒中所成的像CD的高度是________ cm.

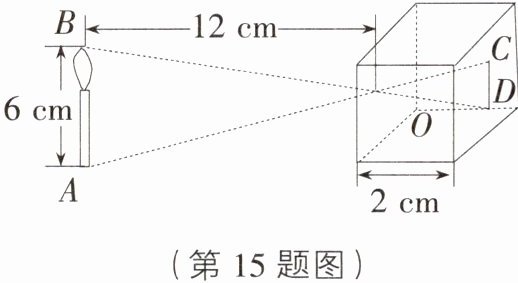
答案： 1 [解析]由题意，得AB//DC，则△ABO∽△CDO，故$\frac{AB}{DC}=\frac{6}{DC}=\frac{12}{2}$，解得DC = 1 cm.

16. [河南新乡封丘期中]学完了《图形的相似》这一章后，某中学数学实践小组决定利用所学知识去测量一古建筑AB的高度(如图1).如图2，在地面BC上取E，G两点，分别竖立两根高为2 m的标杆EF和GH，两标杆间隔EG为23 m，并且古建筑AB、标杆EF和GH在同一竖直平面内，从标杆EF后退2 m到D处，从D处观察点A，A，F，D三点成一线；从标杆GH后退4 m到C处，从C处观察点A，A，H，C三点也成一线.请根据以上测量数据，帮助实践小组求出该古建筑的高度.

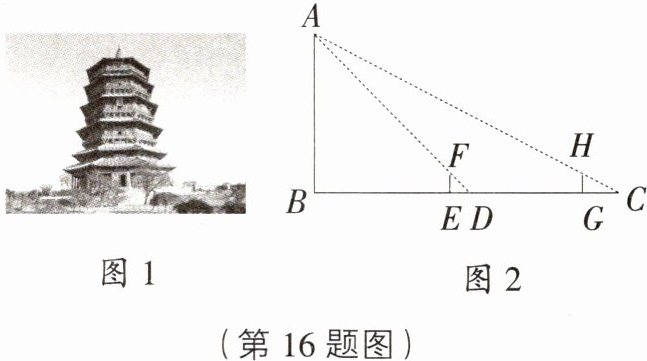
答案： [解析]设BE = y m，由题意，可知△ABD∽△FED，△ABC∽△HGC，
∴$\frac{EF}{AB}=\frac{ED}{BD}$，$\frac{GC}{BC}=\frac{HG}{AB}$，
∵EF = HG = 2 m，
∴$\frac{ED}{BD}=\frac{GC}{BC}$，
∴$\frac{2}{2 + y}=\frac{4}{4 + 23 + y}$，解得y = 23，
∵$\frac{ED}{BD}=\frac{EF}{AB}$，
∴$\frac{2}{23 + 2}=\frac{2}{AB}$，解得AB = 25 m.

17. [河北中考]图1是装了液体的高脚杯示意图(数据如图)，用去一部分液体后如图2所示，此时液面AB=( )

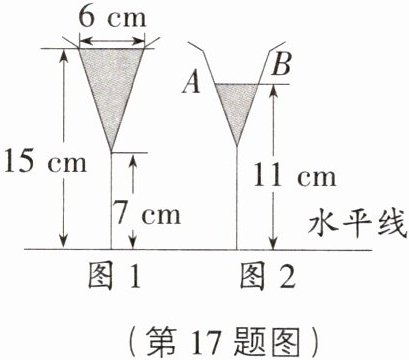
A. 1 cm
B. 2 cm
C. 3 cm
D. 4 cm

答案：
C [解析]如图，过点O作OM⊥CD，垂足为M，过点O'作O'N⊥AB，垂足为点N，
∵CD//AB，
∴△CDO∽△ABO'，即相似比为$\frac{CD}{AB}$，
∴$\frac{CD}{AB}=\frac{OM}{O'N}$，
∵OM = 15 - 7 = 8(cm)，O'N = 11 - 7 = 4(cm)，
∴$\frac{6}{AB}=\frac{8}{4}$，
∴AB = 3 cm.