《2025年考点集训与满分备考九年级数学全一册下人教版》

9. 如图，在△ABC中，CD是边AB上的高，若$\frac{CB}{AC}=\frac{CD}{AD}$，则下列结论正确的有( )
①△ADC∽△ACB；
②△BDC∽△BCA；
③△ADC∽△CDB；
④CD²=BD·AD


A. 1个
B. 2个
C. 3个
D. 4个

答案： 9.D　[解析]
∵CD是边AB上的高，
∴∠ADC=∠CDB=90°,
　又
∵$\frac{CB}{AC}$=$\frac{CD}{AD}$,
∴△ADC∽△CDB,故③正确,
∴$\frac{CD}{BD}$=$\frac{AD}{CD}$
∴CD²=BD.AD,
　故④正确，
∵△ADC∽△CDB,
∴∠A=∠DCB,∠ACD=∠B,
　又
∵∠B=∠B,∠A=∠A,
∴△ADC∽△ACB,△BDC∽△BCA,故①②正确,
∴正确的有4个.

10. 如图，在矩形ABCD中，作DF⊥AC，垂足为F，延长DF交边AB于点E，在图中一定和△DFC相似的三角形个数是 .

答案：
10.5　[解析]如图,①
∵四边形
ABCD是矩形,.,AB//CD,
∴△DFC∽△EFA.②
∵四边形ABCD是矩形，
∴∠CDA=90°.又DF⊥AC,
∴∠DFC=
　90°,
∴∠1=∠2,
∴△DFC∽△AFD.③:.∠1=∠1,∠CFD=∠CDA=90°,
∴△DFC∽△ADC.④同理,△DFC∽△EAD.⑤△DFC∽△CBA.
　综上所述，在图中一定和△DFC相似的三角形个数是5.

11. [河北模拟]已知如图1、图2中各有两个三角形，其边长和角的度数已在图上标注，图2中AB，CD交于点O，对于各图中的两个三角形而言，下列说法正确的是( )
A. 只有1相似
B. 只有2相似
C. 都相似
D. 都不相似

答案： 11.C　　[解析]对于图1,180°−75°−35°=70°,则两个三角形中有两组角对应相等，所以图1中的两个三角形相似;对于图2,由于$\frac{4}{3}$=$\frac{8}{6}$,
　∠AOC=∠DOB,
∴△AOC∽△DOB.

12. [河南周口月考]如图，要使△ABC∽△DAC，只需要添加一个条件即可，这个条件不可能是( )
A. ∠B=∠DAC
B. $\frac{AB}{AD}=\frac{AC}{DC}$
C. AC²=DC·BC
D. ∠BAC=∠ADC

答案： 12.B　[解析]由题意可得∠C=∠C,..A.当∠B=∠DAC时,
能判定△ABC∽△DAC;B.当$\frac{AB}{AD}$=
　$\frac{AC}{DC}$时,不能判定△ABC∽△DAC;
C.当AC²=DC.BC时,有$\frac{AC}{DC}$$\frac{BC}{AC}$,能判定△ABC∽△DAC;D.当∠BAC=
　∠ADC时,能判定△ABC∽△DAC.

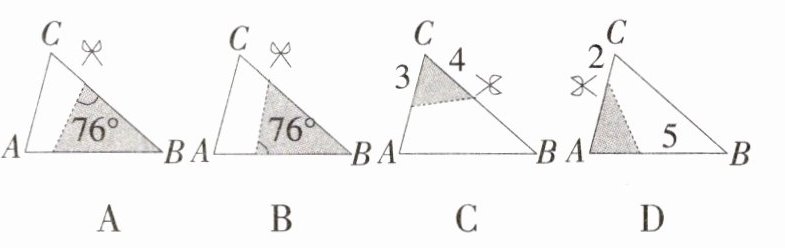
13. [北京清华附中考]如图，△ABC中，∠A=76°，AB=8，AC=6.将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是( )

答案： 13.C　[解析]A.阴影三角形与原三角形有两个角相等，故两三角形相似;B.阴影三角形与原三角形有两个角相等，故两三角形相似;C.两三角形的对应边不成比例，故两三角形不相似;D.阴影三角形中,∠A的两边长分别为6−2=4,8−5=3,则两三角形对应边成比例且夹角相等，故两三角形相似,

14. [吉林长春108中月考]如图，若∠1=∠2，则下列各式不能证明△ABC∽△ADE的是( )

A. $\frac{AD}{AB}=\frac{DE}{BC}$
B. ∠D=∠B
C. $\frac{AD}{AB}=\frac{AE}{AC}$
D. ∠E=∠C

答案： 14.A　　[解析]
∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
∴∠DAE=
　∠BAC,若∠D=∠B或∠E=∠C,根据两角对应相等，两个三角形相似，所以B,D正确，因为两边对应成比例，两个三角形相似，所以C正确，
A不具备相似的条件.

15. [安徽六安汇文中学月考]如图，在△ABC中，∠BAC=90°，AD⊥BC，则图中相似三角形共有( )

A. 1对
B. 2对
C. 3对
D. 4对

答案： 15.C　　[解析]..AD⊥BC,
∴∠ADC=
　90°,
∵∠BAC=90°.∠ADC=∠BAC=
　∠ADB,又
∵∠B=∠B,
∴△BAD∽△BCA,
∵∠ADC=∠BAC,∠C=∠C,
∴△CAD∽△CBA,
∴△BAD∽△ACD,
∴共有3对.

16. [陕西咸阳兴平期中]如图，在四边形ABCD中，已知∠ADC=∠BAC，那么补充下列条件后不能判定△ADC和△BAC相似的是( )

A. CA平分∠BCD
B. $\frac{AD}{AB}=\frac{DC}{AC}$
C. AC²=BC·CD
D. ∠DAC=∠ABC

答案： 16.C　　[解析]在△ADC和△BAC 中,∠ADC=∠BAC,如果补充AC²=
BC.CD,则不满足相似的判定条件，故不能判定△ADC和△BAC相似,