《2025年考点集训与满分备考九年级数学全一册下人教版》

6. 如图，是用卡钳测量容器内径的示意图，量得卡钳上A，D两端点的距离为5 cm，$\frac{AO}{OC}=\frac{DO}{OB}=\frac{2}{5}$，则容器的内径BC的长为____ cm.

答案： $\frac{25}{2}$ [解析]
∵$\frac{AO}{OC}=\frac{DO}{OB}=\frac{2}{5}$，∠AOD = ∠BOC，
∴△AOD∽△COB，
∴$\frac{AD}{BC}=\frac{AO}{CO}=\frac{2}{5}$，又AD = 5 cm，
∴BC = $\frac{5}{2}AD=\frac{25}{2}$ cm.

7. 如图所示，一条河流的两岸互相平行，沿南岸有一排大树，每隔4 m一棵，沿北岸有一排电线杆，每两根电线杆之间的距离为80 m，一同学站在距南岸9 m的点P处，正好北岸相邻的两根电线杆被南岸的5棵树遮挡住，那么这条河流的宽度是______ m.

答案：
36 [解析]如图，设这条河流的宽度是h m，AB//CD，AB = 16 m，P到AB的距离是9 m，
∴△ABP∽△DCP，
∴$\frac{16}{80}=\frac{9}{h + 9}$，解得h = 36.

8. 《九章算术》中记载了一种测距的方法.如图，有座塔在河流北岸的点E处，一棵树位于河流南岸的点A处，从点A处开始，在河南岸立4根标杆，以这4根标杆为顶点，组成边长为10 m的正方形ABCD，且A，D，E三点在一条直线上，在标杆B处观察塔E，视线BE与边DC相交于点F，如果测得FC=4 m，那么塔与树的距离AE为________ m.

答案： 25 [解析]
∵四边形ABCD是正方形，边长为10 m，
∴AD = CD = BC = 10 m，FD = CD - CF = 6 m，BC//AD，
∴△FDE∽△FCB，
∴$\frac{DE}{CB}=\frac{DF}{CF}$，即$\frac{DE}{10}=\frac{6}{4}$，DE = 15 m，
∴AE = DE + AD = 25 m.

9. 在阳光下，一名同学测得一根长为1 m的竹竿的影长为0.8 m，同时另一名同学测得一棵树落在学校墙壁上的影长为1.2 m，此树落在地面上的影长为2.4 m，则此树的高度为_______ m.

答案： 4.2 [解析]设树落在地面上的影长对应的高度是x m，则$\frac{x}{2.4}=\frac{1}{0.8}$，解得x = 3.
∵树落在学校墙壁上的影长为1.2 m，
∴此树的高度为3 + 1.2 = 4.2(m).

10. [陕西咸阳秦都区月考]如图，小明探究课本“综合与实践”板块“制作视力表”的相关内容：当测试距离为5 m时，标准视力表中最大的“E”字高度为72.7 mm，当测试距离为3 m时，最大的“E”字高度为( )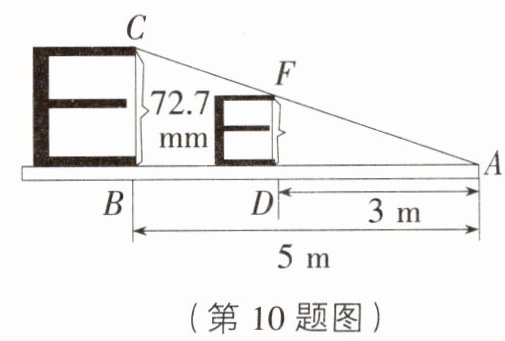
A. 4.36 mm
B. 29.08 mm
C. 43.62 mm
D. 121.17 mm

答案： C [解析]由题意，得CB//DF，
∴△ADF∽△ABC，
∴$\frac{DF}{BC}=\frac{AD}{AB}$，
∵AD = 3 m，AB = 5 m，BC = 72.7 mm，
∴$\frac{DF}{72.7}=\frac{3}{5}$，DF = 43.62 mm.

11. [北京东城区期末]如图，在圆形花圃中有两条笔直的小径，两端都在花圃边界上，分别记为AC，BD，设交点为P，点C，D之间有一座假山，为了测量C，D之间的距离，小明已经测量了线段AP和PD的长度，只需再测量一条线段的长度，就可以计算C，D之间的距离.小明应该测量的是( )

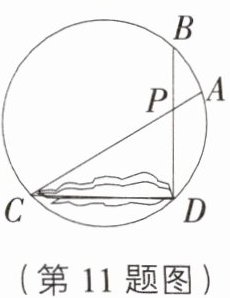
A. 线段BP
B. 线段CP
C. 线段AB
D. 线段AD

答案： C [解析]在题图上连接AB.
∵∠DCP = ∠ABP，∠DPC = ∠APB，
∴△APB∽△DPC，AP:DP = AB:DC.
∴只需再测量线段AB的长度，就可以计算C，D之间的距离.

12. [河北唐山遵化期中]如图，小明在A时测得某树的影长为8 m，B时又测得该树的影长为2 m，若两次日照的光线互相垂直，则树的高度为( )

A. 2 m
B. 4 m
C. 6 m
D. 8 m

答案：
B [解析]根据题意，作△EFC，如图，树高为CD，且∠ECF = 90°，ED = 2 m，FD = 8 m.
∵∠E + ∠F = 90°，∠E + ∠ECD = 90°，
∴∠ECD = ∠F，
∴△EDC∽△CDF，
∴$\frac{ED}{CD}=\frac{CD}{DF}$，即CD² = ED·FD = 2×8 = 16，
∴CD = 4 m.