第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
17. 反比例函数$y=\frac{k - 3}{x}$的图象位于第二、四象限,则$k$的取值范围是_____.
答案:
$k\lt3$ [解析]$\because$反比例函数$y=\frac{k - 3}{x}$的图象位于第二、四象限,$\therefore k - 3\lt0$,解得$k\lt3$.
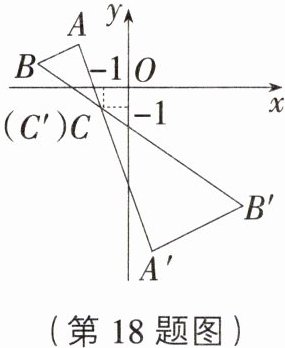
18. 如图,在$\triangle ABC$中,三个顶点的坐标分别是$A(-2,2)$,$B(-4,1)$,$C(-1,-1)$.以点$C$为位似中心,在$x$轴下方作$\triangle ABC$的位似图形$\triangle A'B'C'$,并把$\triangle ABC$的边长放大为原来的2倍,那么点$A'$的坐标为_______.

答案:
$(1,-7)$ [解析]把$\triangle ABC$先向右平移$1$个单位长度,再向上平移$1$个单位得到$\triangle A_{1}B_{1}C_{1}$,此时点$C$平移到原点,点$A$平移后的对应点$A_{1}$的坐标为$(-1,3)$,以原点为位似中心,把$\triangle A_{1}B_{1}C_{1}$的边长放大为原来的$2$倍,在位似中心异侧的对应点的坐标为$(2,-6)$,然后把点$(2,-6)$先向左平移$1$个单位长度,再向下平移$1$个单位长度,则点$A'$的坐标为$(1,-7)$.
19. 如图,在$\square ABCD$中,$AC$,$BD$相交于点$O$,$E$是$OA$的中点,连接$BE$并延长交$AD$于点$F$.
(1)$\frac{FD}{AF}=$_________;
(2)若$\triangle AEF$的面积为4,则$\square ABCD$的面积为______.

(1)$\frac{FD}{AF}=$_________;
(2)若$\triangle AEF$的面积为4,则$\square ABCD$的面积为______.

答案:
(1)$2$ (2)$96$
[解析](1)$\because$四边形$ABCD$是平行四边形,$\therefore OA = OC$,$AD// BC$,$AD = BC$,$\because$点$E$是$OA$的中点,$\therefore CE = 3AE$,$\because AF// BC$,$\therefore\triangle AEF\sim\triangle CEB$,$\therefore\frac{BC}{FA}=\frac{CE}{AE}=3$,$\therefore BC = 3AF$,$\therefore FD = 2AF$,$\therefore\frac{FD}{AF}=2$;
(2)$\because\triangle AEF\sim\triangle CEB$,$\therefore\frac{S_{\triangle AEF}}{S_{\triangle CEB}}=(\frac{1}{3})^{2}=\frac{1}{9}$,$\therefore\triangle CEB$的面积$=9\times4 = 36$,$\because CE = 3AE$,$\therefore S_{\triangle ABE}=\frac{1}{3}S_{\triangle CEB}=12$,$\therefore S_{\triangle ABC}=12 + 36 = 48$,$\therefore$平行四边形$ABCD$的面积$=2S_{\triangle ABC}=2\times48 = 96$.
[解析](1)$\because$四边形$ABCD$是平行四边形,$\therefore OA = OC$,$AD// BC$,$AD = BC$,$\because$点$E$是$OA$的中点,$\therefore CE = 3AE$,$\because AF// BC$,$\therefore\triangle AEF\sim\triangle CEB$,$\therefore\frac{BC}{FA}=\frac{CE}{AE}=3$,$\therefore BC = 3AF$,$\therefore FD = 2AF$,$\therefore\frac{FD}{AF}=2$;
(2)$\because\triangle AEF\sim\triangle CEB$,$\therefore\frac{S_{\triangle AEF}}{S_{\triangle CEB}}=(\frac{1}{3})^{2}=\frac{1}{9}$,$\therefore\triangle CEB$的面积$=9\times4 = 36$,$\because CE = 3AE$,$\therefore S_{\triangle ABE}=\frac{1}{3}S_{\triangle CEB}=12$,$\therefore S_{\triangle ABC}=12 + 36 = 48$,$\therefore$平行四边形$ABCD$的面积$=2S_{\triangle ABC}=2\times48 = 96$.
三、解答题(共66分)
20. (5分)[浙江杭州采荷中学期中]如图,直线$l_{1}// l_{2}// l_{3}$,若$AB = 6$,$BC = 10$,$EF = 9$,求$DE$的长.
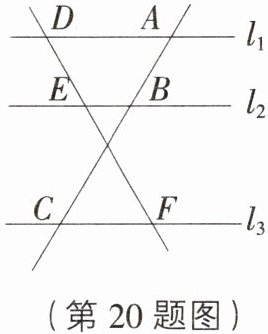
20. (5分)[浙江杭州采荷中学期中]如图,直线$l_{1}// l_{2}// l_{3}$,若$AB = 6$,$BC = 10$,$EF = 9$,求$DE$的长.

答案:
[解析]$\because l_{1}// l_{2}// l_{3}$,$AB = 6$,$BC = 10$,$\therefore\frac{DE}{EF}=\frac{AB}{BC}=\frac{6}{10}=\frac{3}{5}$,$\because EF = 9$,$\therefore DE=\frac{27}{5}$.
21. (8分)[河南南阳邓州期末]如图,已知$CD$是$Rt\triangle ABC$斜边$AB$上的中线,过点$D$作$AC$的平行线,过点$C$作$CD$的垂线,两线相交于点$E$.
(1)求证:$\triangle ABC\backsim\triangle DEC$;
(2)若$AB = 8$,$CE = 3$,求$\triangle ABC$的周长.
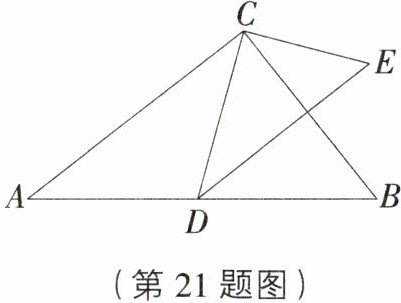
(1)求证:$\triangle ABC\backsim\triangle DEC$;
(2)若$AB = 8$,$CE = 3$,求$\triangle ABC$的周长.

答案:
[解析](1)$\because DC\perp CE$,$\therefore\angle DCE = 90^{\circ}$,$\therefore\angle ACB=\angle DCE$.$\because AC// DE$,$\therefore\angle ACD=\angle CDE$,又$\because CD$是$Rt\triangle ABC$斜边$AB$上的中线,$\therefore CD = AD$,$\therefore\angle ACD=\angle A$,$\therefore\angle A=\angle CDE$,$\therefore\triangle ABC\sim\triangle DEC$;
(2)$\because CD$是$Rt\triangle ABC$斜边$AB$上的中线,$\therefore CD=\frac{1}{2}AB = 4$,在$Rt\triangle DCE$中,$DE=\sqrt{CD^{2}+CE^{2}}=\sqrt{4^{2}+3^{2}} = 5$,$\because\triangle ABC\sim\triangle DEC$,$\therefore\frac{AC}{CD}=\frac{BC}{EC}=\frac{AB}{DE}$,即$\frac{AC}{4}=\frac{BC}{3}=\frac{8}{5}$,$\therefore AC=\frac{32}{5}$,$BC=\frac{24}{5}$,$\therefore\triangle ABC$的周长$=\frac{32}{5}+\frac{24}{5}+8=\frac{96}{5}$.
(2)$\because CD$是$Rt\triangle ABC$斜边$AB$上的中线,$\therefore CD=\frac{1}{2}AB = 4$,在$Rt\triangle DCE$中,$DE=\sqrt{CD^{2}+CE^{2}}=\sqrt{4^{2}+3^{2}} = 5$,$\because\triangle ABC\sim\triangle DEC$,$\therefore\frac{AC}{CD}=\frac{BC}{EC}=\frac{AB}{DE}$,即$\frac{AC}{4}=\frac{BC}{3}=\frac{8}{5}$,$\therefore AC=\frac{32}{5}$,$BC=\frac{24}{5}$,$\therefore\triangle ABC$的周长$=\frac{32}{5}+\frac{24}{5}+8=\frac{96}{5}$.
22. (8分)[上海普陀区期中]如图,在平面直角坐标系$xOy$中,反比例函数$y=\frac{k}{x}(k\neq0)$的图象与正比例函数$y = 2x$的图象相交于横坐标为1的点$A$.
(1)求这个反比例函数的解析式;
(2)如图,已知$B$是正比例函数图象在第一象限内的一点,过点$B$作$BC\perp x$轴,垂足为点$C$,$BC$与反比例函数图象交于点$D$,如果$AB = AC$,求点$D$的坐标.
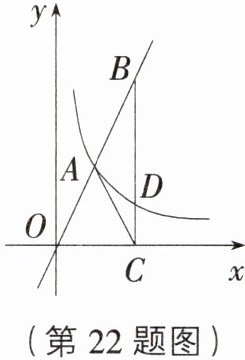
(1)求这个反比例函数的解析式;
(2)如图,已知$B$是正比例函数图象在第一象限内的一点,过点$B$作$BC\perp x$轴,垂足为点$C$,$BC$与反比例函数图象交于点$D$,如果$AB = AC$,求点$D$的坐标.

答案:
[解析](1)把$x = 1$代入$y = 2x$,得$y = 2$,$\therefore$点$A$的坐标为$(1,2)$,把点$A$的坐标代入$y=\frac{k}{x}$($k\neq0$),得$k = 1\times2 = 2$,即反比例函数的解析式为$y=\frac{2}{x}$;
(2)如图,过点$A$作$AE\perp BC$于点$E$.$\because BC\perp x$轴,$\therefore AE// x$轴,$\because A(1,2)$,$\therefore CE = 2$,$\because AC = AB$,$AE\perp BC$,$\therefore CE = BE = 2$,$\therefore$点$B$的纵坐标为$4$,把$y = 4$代入$y = 2x$,得$4 = 2x$,解得$x = 2$,即点$B$的坐标为$(2,4)$,$\because$点$D$的横坐标为$2$,把$x = 2$代入$y=\frac{2}{x}$,得$y = 1$,$\therefore D(2,1)$.
(2)如图,过点$A$作$AE\perp BC$于点$E$.$\because BC\perp x$轴,$\therefore AE// x$轴,$\because A(1,2)$,$\therefore CE = 2$,$\because AC = AB$,$AE\perp BC$,$\therefore CE = BE = 2$,$\therefore$点$B$的纵坐标为$4$,把$y = 4$代入$y = 2x$,得$4 = 2x$,解得$x = 2$,即点$B$的坐标为$(2,4)$,$\because$点$D$的横坐标为$2$,把$x = 2$代入$y=\frac{2}{x}$,得$y = 1$,$\therefore D(2,1)$.
23. (9分)[安徽合肥包河区二模]如图,是由边长为1的小正方形组成的网格,已知格点正方形$ABCD$及格点$O$.
(1)将正方形$ABCD$向左平移2个单位长度,再向上平移2个单位长度,得到正方形$A_{1}B_{1}C_{1}D_{1}$;
(2)以$O$为位似中心,在点$O$的同侧画出正方形$A_{1}B_{1}C_{1}D_{1}$的位似图形$A'B'C'D'$,使位似比为$1:2$;
(3)除了点$O$外,正方形$A'B'C'D'$和正方形$A_{1}B_{1}C_{1}D_{1}$还有位似中心吗?如果有,请找出来.
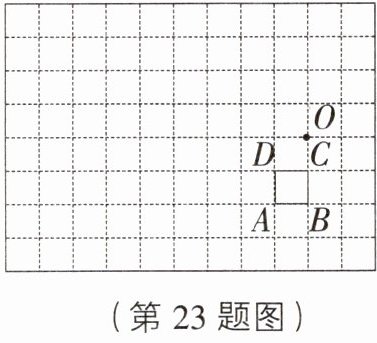
(1)将正方形$ABCD$向左平移2个单位长度,再向上平移2个单位长度,得到正方形$A_{1}B_{1}C_{1}D_{1}$;
(2)以$O$为位似中心,在点$O$的同侧画出正方形$A_{1}B_{1}C_{1}D_{1}$的位似图形$A'B'C'D'$,使位似比为$1:2$;
(3)除了点$O$外,正方形$A'B'C'D'$和正方形$A_{1}B_{1}C_{1}D_{1}$还有位似中心吗?如果有,请找出来.

答案:
[解析](1)如图,正方形$A_{1}B_{1}C_{1}D_{1}$即为所求;
(2)如图,正方形$A'B'C'D'$即为所求;
(3)除了点$O$外,正方形$A'B'C'D'$和正方形$A_{1}B_{1}C_{1}D_{1}$还有位似中心,如图,点$P$为位似中心.
(2)如图,正方形$A'B'C'D'$即为所求;
(3)除了点$O$外,正方形$A'B'C'D'$和正方形$A_{1}B_{1}C_{1}D_{1}$还有位似中心,如图,点$P$为位似中心.
查看更多完整答案,请扫码查看


