《2025年考点集训与满分备考九年级数学全一册下人教版》

1. 如图，为估算学校的旗杆的高度，身高1.6 m的小红同学沿着旗杆在地面的影子AB由A向B走去，当她走到点C处时，她的影子的顶端正好与旗杆的影子的顶端重合，此时测得AC=2 m，BC=8 m，则旗杆的高度是( )


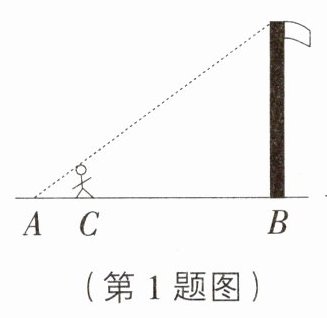
A. 6.4 m
B. 7 m
C. 8 m
D. 9 m

答案： C [解析]设旗杆的高度为h m，由题意，得$\frac{1.6}{h}=\frac{2}{2 + 8}$，解得h = 8.

2. 如图，为了测量塔AB的高度，数学兴趣小组根据光的反射定理(图中∠1=∠2)，把一面镜子放在点C处，然后观测者沿着直线BC后退到点D.这时恰好在镜子里看到塔顶A，此时量得CD=4 m，BD=94 m，观测者目高ED=1.6 m，则塔AB的高度为( )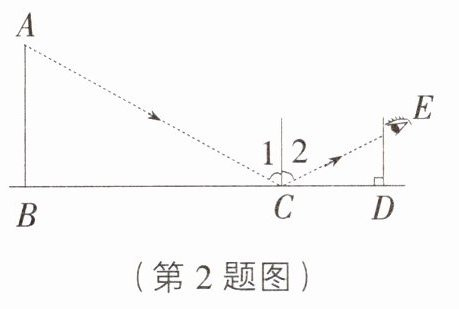
A. 35 m
B. 36 m
C. 37 m
D. 38 m

答案： B [解析]
∵CD = 4 m，BD = 94 m，
∴BC = BD - CD = 90 m.由题意知∠1 = ∠2，
∴∠ACB = ∠ECD，∠ABC = ∠EDC = 90°，
∴△ABC∽△EDC.
∴$\frac{AB}{ED}=\frac{BC}{DC}$，
∴$\frac{AB}{1.6}=\frac{90}{4}$，AB = 36.

3. 小明在测量楼高时，先测出楼房落在地面上的影长BA为15 m(如图)，然后在A处立一根高2 m的标杆，测得标杆的影长AC为3 m，则楼高为____.

答案： 10 m [解析]
∵$\frac{标杆的高}{标杆的影长}=\frac{楼高}{楼影长}$，即$\frac{2}{3}=\frac{楼高}{15}$，
∴楼高为10 m.

4. 铁路道口的栏杆如图，其A，B两端到旋转支点C的距离分别为AC=1.2 m，BC=15 m.栏杆在水平状态下到地面的距离CD为1.3 m，栏杆绕点C转动，当A端下降至离地距离AE为0.9 m时，B端到地面的距离BF为多少米?

答案：
[解析]如图，延长EA，交A'B'于点A'，由题意，可得AC = 1.2 m，BC = 15 m，AA' = 1.3 - 0.9 = 0.4(m)，AA'⊥A'B'，BB'⊥A'B'，AA'//BB'，
∴△A'AC∽△B'BC，
∴$\frac{AC}{BC}=\frac{AA'}{BB'}$，
∴$\frac{1.2}{15}=\frac{0.4}{BB'}$，BB' = 5 m，
∴BF = 5 + 1.3 = 6.3(m).

5. 如图，A，B两地之间有一池塘，要测量A，B两地之间的距离，选择一点O，连接AO并延长到点C，使OC=$\frac{1}{2}AO$，连接BO并延长到点D，使OD=$\frac{1}{2}BO$.测得C，D间距离为30 m，则A，B两地之间的距离为( )

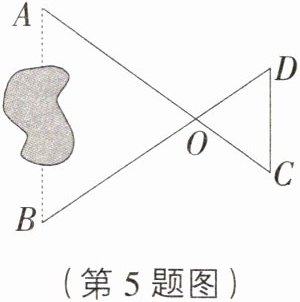
A. 30 m
B. 45 m
C. 60 m
D. 90 m

答案： C [解析]
∵在△AOB和△COD中，$\frac{OA}{OC}=\frac{OB}{OD}=2$，且∠AOB = ∠COD，
∴△AOB∽△COD，
∴$\frac{AB}{CD}=2$.又
∵CD = 30 m，
∴AB = 60 m.