《2025年考点集训与满分备考九年级数学全一册下人教版》

7. 一段公路路面的坡度i = 1:2.4，如果某人沿着这段公路向上行走了130 m，那么此人升高了 ____ m.

答案： 50　[解析]设此人升高了xm，
∵坡度i为1:2.4，
∴此人行走的水平宽度为2.4xm，由勾股定理，得x² + (2.4x)² = 130²，解得x = 50(负值已舍去)，即此人升高了50m。

8. 如图，某水库大坝的横断面是四边形ABCD，AD//BC，坝顶宽AD = 2.5 m，坝高AE = DF = 4 m，背水坡AB的坡度是1:1，迎水坡CD的坡度是1:1.5，求坝底宽BC.

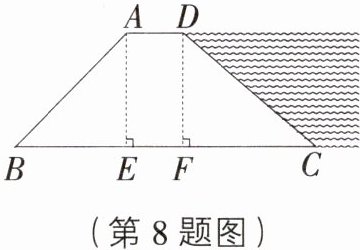
答案： [解析]
∵坡CD的坡度是1:1.5，DF = 4m，
∴FC = 1.5DF = 6m，
∵坡AB的坡度是1:1，AE = 4m，
∴BE = AE = 4m，
∵AD//BC，AE//DF，AE⊥BC，
∴四边形AEFD为矩形，
∴EF = AD = 2.5m，
∴BC = BE + EF + FC = 4 + 2.5 + 6 = 12.5(m)，即坝底宽BC的长为12.5m。

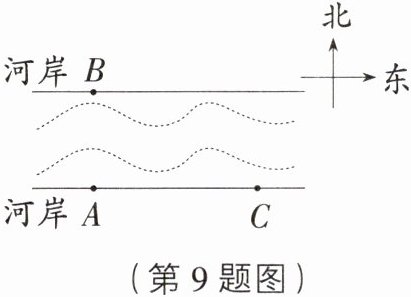
9. [河北石家庄长安区模拟]如图为东西流向且河岸平行的一段河道，点A，B分别为两岸上一点，且点B在点A正北方向，由点A向正东方向走a m到达点C，此时测得点B在点C的北偏西55°方向上，则河宽AB的长为 ( )

A. atan55° m
B. $\frac{a}{\cos55^{\circ}}$ m
C. $\frac{a}{\tan35^{\circ}}$ m
D. $\frac{a}{\tan55^{\circ}}$ m

答案：
9.D　[解析]如图，连接AB，BC，由题意得，∠BAC = 90°，∠ABC = 55°，AC = am，
∴tan∠ABC = tan55° = $\frac{AC}{AB}$，
∴AB = $\frac{AC}{tan55°}$ = $\frac{a}{tan55°}$m。

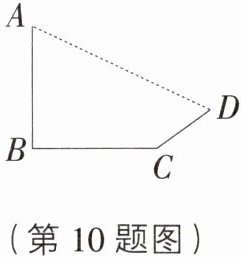
10. [难点][陕西西安85中期中]如图，小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上，量得CD = 8 m，BC = 20 m，CD与地面成30°角，且此时测得高为1 m的木杆的影长为2 m，则电线杆的高度为 ( )

A. 9 m
B. 28 m
C. (7+$\sqrt{3}$) m
D. (14 + 2$\sqrt{3}$) m

答案：
10.D　[解析]如图，延长AD交BC的延长线于F点，作DE⊥CF于E点。由题易得DE = 8×sin30° = 4m，CE = 8×cos30° = 4$\sqrt{3}$m。
∵测得高为1m的木杆的影长为2m。
∴EF = 2DE = 8m，
∴BF = BC + CE + EF = 20 + 4$\sqrt{3}$ + 8 = (28 + 4$\sqrt{3}$)m，
∴电线杆AB的高度为$\frac{1}{2}$×(28 + 4$\sqrt{3}$) = (14 + 2$\sqrt{3}$)m。

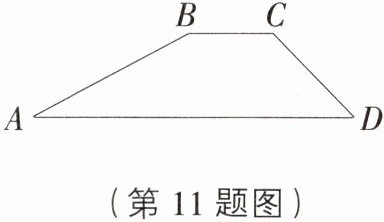
11. [浙江工大附属实验学校模拟]如图是某大坝的横断面，斜坡AB的坡比i = 1:2，背水坡CD的坡比i = 1:1，若坡面CD的长度为6$\sqrt{2}$ m，则斜坡AB的长度为 ________ m.

答案：
11.6$\sqrt{5}$　[解析]如图，过点B作BE⊥AD于点E，过点C作CF⊥AD于点F，则四边形BEFC为矩形。
∴BE = CF，
∵坡CD的坡比i = 1:1，
∴∠D = 45°，
∴CF = $\frac{\sqrt{2}}{2}$CD = $\frac{\sqrt{2}}{2}$×6$\sqrt{2}$ = 6(m)，
∵斜坡AB的坡比i = 1:2，
∴AE = 2BE = 2CF = 12m，由勾股定理，得AB = $\sqrt{AE^{2}+BE^{2}}$ = $\sqrt{12^{2}+6^{2}}$ = 6$\sqrt{5}$(m)。

12. [重点][云南大学附中月考]如图，一艘轮船从位于灯塔C的北偏东60°方向，距离灯塔60 n mile的小岛A出发，沿正南方向航行一段时间后，到达位于灯塔C的南偏东45°方向上的B处，这时轮船B与小岛A的距离约是____ n mile. (结果保留整数，$\sqrt{3}$≈1.732)

答案：
12.82　[解析]设AB与CD交于点D，如图。由已知可得AC = 60n mile，∠ACD = 90° - 60° = 30°，
∴AD = $\frac{1}{2}$AC = 30n mile，
∴CD = AC·cos30° = 30$\sqrt{3}$(n mile)，
∵∠BCD = 90° - 45° = 45°，∠ADC = 90°，
∴∠BCD = ∠CBD = 45°，
∴BD = CD = 30$\sqrt{3}$n mile，
∴AB = AD + BD = 30 + 30$\sqrt{3}$≈30 + 30×1.732 = 81.96≈82(n mile)。

13. [河南名校联考]"青山绿水，生态农业."某地需引水修建水库，既可蓄水灌溉，又可美化环境.据了解，水库C修建在水源A的正东方向，在水源A的北偏东75°方向有一古迹B，B与A相距14 km，其中水库C在古迹B的东南方向.
(1)若在水源A与水库C之间修建一条水渠，求该水渠的最短长度；
(2)在古迹B的西南方向5 km处有一古墓群，为了保护文物，不破坏古墓，在古墓群周围1 km范围内不得进行任何土工作业，判断按照(1)中的方式修建水渠是否合理，并说明理由. (结果保留一位小数.参考数据:sin15°≈0.26，cos15°≈0.97，$\sqrt{2}$≈1.41)

答案：
13.[解析]
(1)如图，过点B作BD⊥AC于点D。由题意，得∠BAD = 15°，∠DBC = ∠DCB = 45°，AB = 14km，BD = DC，在Rt△ADB中，BD = AB·sin15°≈14×0.26 = 3.64(km)，AD = AB·cos15°≈14×0.97 = 13.58(km)，
∴CD = BD = 3.64(km)，
∴AC = AD + DC = 13.58 + 3.64≈17.2(km)，根据“两点之间，线段最短”，可知线段AC的长即为所求，即该水渠的最短长度约为17.2km；
(2)按照
(1)中的方式修建水渠不合理，理由如下:如图，过点B作BE⊥BC交AC于点E，由
(1)知，∠DCB = 45°，CD≈3.64km，
∴CE = 2CD≈7.28km，
∴BE = CE·sin45° = 7.28×$\frac{\sqrt{2}}{2}$≈7.28×$\frac{1.41}{2}$≈5.1(km)，
∵5.1 - 5 = 0.1(km)，0.1km＜1km，
∴有破坏文物的可能，即按照
(1)中的方式不合理。