《2025年考点集训与满分备考九年级数学全一册下人教版》

1. 已知Rt△ABC中，∠ACB=90°，AC=3，AB=5，则cosA的值为（ ）
A. $\frac{3}{5}$
B. $\frac{4}{3}$
C. $\frac{3}{4}$
D. $\frac{4}{5}$

答案： A [解析]在Rt△ABC中，∠ACB = 90°，
∴cos A = $\frac{AC}{AB}$ = $\frac{3}{5}$。

2. 如图，在Rt△ABC中，∠C=90°，AC=4，cosA=$\frac{4}{5}$，则BC的长为（ ）

A. 3
B. 4
C. 5
D. 6

答案： A [解析]
∵在Rt△ABC中，∠C = 90°，cos A = $\frac{4}{5}$，
∴$\frac{AC}{AB}$ = $\frac{4}{5}$，即$\frac{4}{AB}$ = $\frac{4}{5}$，解得AB = 5。在Rt△ABC中，由勾股定理可得BC = $\sqrt{AB^{2}-AC^{2}}$ = $\sqrt{5^{2}-4^{2}}$ = 3。

3. 在Rt△ABC中，∠A=90°，AB=3，BC=4，则cosB=_______.

答案： $\frac{3}{4}$ [解析]在Rt△ABC中，∠A = 90°，AB = 3，BC = 4，
∴cos B = $\frac{AB}{BC}$ = $\frac{3}{4}$。

4. 如图，在Rt△ABC中，∠C=90°，AC=3，AB=5，求sinA·cosA的值.

答案： [解析]在Rt△ABC中，∠C = 90°，AC = 3，AB = 5，由勾股定理，得BC = $\sqrt{AB^{2}-AC^{2}}$ = $\sqrt{5^{2}-3^{2}}$ = 4，
∴sin A = $\frac{BC}{AB}$ = $\frac{4}{5}$，cos A = $\frac{AC}{AB}$ = $\frac{3}{5}$，
∴sin A·cos A = $\frac{4}{5}$×$\frac{3}{5}$ = $\frac{12}{25}$。

5. 在Rt△ABC中，若各边长都扩大为原来的3倍，则锐角A的正切值（ ）
A. 扩大为原来的3倍
B. 缩小为原来的$\frac{1}{3}$
C. 不变
D. 以上都不对

答案： C [解析]由锐角三角函数的定义可知，将Rt△ABC中的各边长都扩大为原来的3倍，∠A的对边与邻边的比值不变，因此锐角A的正切值不变。

6. 在Rt△ABC中，∠C=90°，AB=5，BC=3，则tanA=（ ）
A. $\frac{3}{4}$
B. $\frac{3}{5}$
C. $\frac{4}{5}$
D. $\frac{4}{3}$

答案： A [解析]
∵AB = 5，BC = 3，∠C = 90°，
∴AC = $\sqrt{5^{2}-3^{2}}$ = 4，
∴tan A = $\frac{BC}{AC}$ = $\frac{3}{4}$。

7. 正方形网格中，∠AOB如图放置，则tan∠AOB的值为__________.

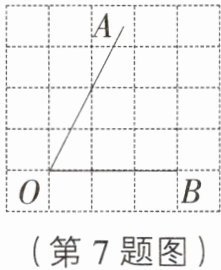
答案：
2 [解析]如图，tan∠AOB = $\frac{CD}{OD}$ = 2。

8. 在△ABC中，∠C=90°，AB=10，tanA=$\frac{3}{4}$，则AC的长为_______.

答案： 8 [解析]在△ABC中，∠C = 90°，tan A = $\frac{BC}{AC}$ = $\frac{3}{4}$，
∴BC = $\frac{3}{4}$AC，由勾股定理，得AB² = AC² + BC²，即10² = AC² + ($\frac{3}{4}$AC)²，
∴AC = 8。

9. [河北石家庄23中期中]在Rt△ABC中，∠C=90°，AB=3，AC=2，则tanA的值为（ ）
A. $\frac{\sqrt{5}}{3}$
B. $\frac{\sqrt{5}}{2}$
C. $\frac{2}{3}$
D. $\frac{2\sqrt{5}}{5}$

答案： B [解析]在Rt△ABC中，∠C = 90°，AB = 3，AC = 2，
∴BC = $\sqrt{AB^{2}-AC^{2}}$ = $\sqrt{5}$，
∴tan A = $\frac{BC}{AC}$ = $\frac{\sqrt{5}}{2}$。

10. [河南驻马店泌阳期中]在Rt△ABC中，∠C=90°，若cosA=$\frac{5}{13}$，BC=12 cm，则AC的长度为( )
A. 3 cm
B. 4 cm
C. 5 cm
D. 6 cm

答案： C [解析]在Rt△ABC中，∠C = 90°，则cos A = $\frac{AC}{AB}$，
∵cos A = $\frac{5}{13}$，
∴$\frac{AC}{AB}$ = $\frac{5}{13}$，设AC = 5x(x＞0)，则AB = 13x。由勾股定理，得(5x)² + 12² = (13x)²，解得x = 1，
∴AC = 5 cm。

11. 重点[陕西西安西北工大附中期中]如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，则（ ）

A. sinA=$\frac{3}{4}$
B. cosA=$\frac{4}{5}$
C. cosB=$\frac{3}{4}$
D. tanB=$\frac{3}{5}$

答案： B [解析]
∵∠C = 90°，AC = 4，BC = 3，
∴AB = $\sqrt{3^{2}+4^{2}}$ = 5，
∴sin A = cos B = $\frac{BC}{AB}$ = $\frac{3}{5}$，cos A = $\frac{AC}{AB}$ = $\frac{4}{5}$，tan B = $\frac{AC}{BC}$ = $\frac{4}{3}$。

12. [河北石家庄外国语学校月考]如图，在4×4的正方形网格中，每个小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则tan∠ACB的值为（ ）


A. $\frac{1}{3}$
B. $\frac{1}{2}$
C. 2
D. 3

答案： C [解析]
∵每个小正方形的边长都是1，
∴AB = 2$\sqrt{2}$，AC = $\sqrt{10}$，BC = $\sqrt{2}$，则AB² + BC² = AC²，
∴△ABC是直角三角形且∠B = 90°，
∴tan∠ACB = $\frac{AB}{BC}$ = 2。