《2025年考点集训与满分备考九年级数学全一册下人教版》

24. （11分）[河北邯郸永年区期末]为了预防“流感”，某学校对教室采用药熏法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量$y(\text{mg})$与药物点燃后的时间$x(\text{min})$成正比例，药物燃尽后，$y$与$x$成反比例（如图所示），已知药物点燃后$6\ \text{min}$燃尽，此时室内每立方米空气中含药量为$12\ \text{mg}$.
（1）求药物燃烧时和药物燃尽后，$y$与$x$之间的函数解析式；
（2）研究表明：空气中每立方米的含药量不低于$6\ \text{mg}$，且持续$5\ \text{min}$以上才能有效杀灭空气中的病菌，请计算说明此次消毒能否有效杀灭空气中的病菌.

答案： ［解析］（1）设药物燃烧时，$y$与$x$之间的函数解析式为$y = mx$，把$(6,12)$代入，得$12 = 6m$，$\therefore m = 2$，$\therefore$药物燃烧时的函数解析式为$y = 2x$（$0\leqslant x\leqslant6$）；设药物燃尽后，$y$与$x$之间的函数解析式为$y=\frac{k}{x}$，把$(6,12)$代入，得$k = xy = 6\times12 = 72$，$\therefore$药物燃尽后的函数解析式为$y=\frac{72}{x}$（$x\gt6$）；
（2）把$y = 6$代入$y = 2x$，得$6 = 2x$，$\therefore x = 3$，把$y = 6$代入$y=\frac{72}{x}$，得$6=\frac{72}{x}$，$\therefore x = 12$，$\because12 - 3 = 9\gt5$，$\therefore$此次消毒能有效杀灭空气中的病菌．

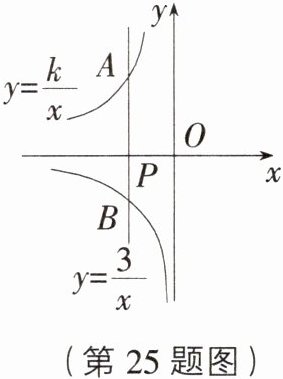
25. （11分）[河北石家庄23中期中]反比例函数$y=\frac{k}{x}(x＜0,k＜0)$和$y=\frac{3}{x}(x＜0)$的图象如图所示，点$P(m,0)$是$x$轴上一动点，过点$P$作直线$AB\perp x$轴，交两图象分别于$A$，$B$两点.
（1）若$m = -1$，线段$AB = 9$时，求点$A$，$B$的坐标及$k$值；
（2）雯雯同学提出一个大胆的猜想：“当$k$一定时，$\triangle OAB$的面积随$m$值的增大而增大.”你认为她的猜想对吗？说明理由.

答案： ［解析］（1）把$x=-1$代入$y=\frac{3}{x}$，得$y=-3$，$\therefore B(-1,-3)$，又$\because AB = 9$，点$A$在第二象限，$\therefore A(-1,6)$．把$A(-1,6)$代入$y=\frac{k}{x}$，得$k=-6$；
（2）雯雯同学的猜想不对．理由如下：把$x = m$代入$y=\frac{3}{x}$，得$y=\frac{3}{m}$，$\therefore B(m,\frac{3}{m})$，把$x = m$代入$y=\frac{k}{x}$，得$y=\frac{k}{m}$，$\therefore A(m,\frac{k}{m})$，$\therefore AB=\frac{k}{m}-\frac{3}{m}=\frac{k - 3}{m}$，又$OP=\vert m\vert=-m$，$\therefore S_{\triangle OAB}=\frac{1}{2}AB\cdot OP=\frac{1}{2}\times\frac{k - 3}{m}\times(-m)=\frac{3 - k}{2}$，即$\triangle OAB$的面积与$m$的值无关，所以雯雯同学的猜想不对．

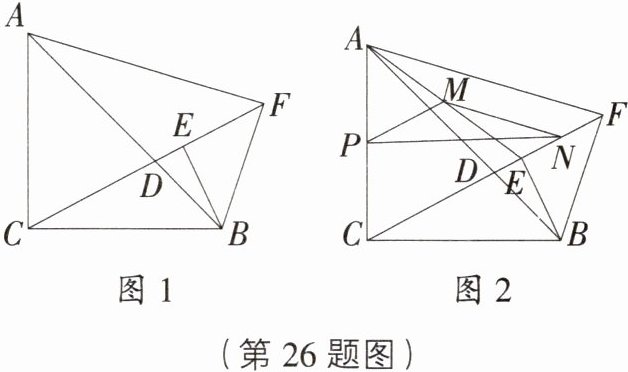
26. （14分）[四川广元中考]如图1，在$\triangle ABC$中，$\angle ACB = 90^{\circ}$，$AC = BC$，点$D$是$AB$边上一点（含端点$A$，$B$），过点$B$作$BE$垂直于射线$CD$，垂足为$E$，点$F$在射线$CD$上，且$EF = BE$，连接$AF$，$BF$.
（1）求证：$\triangle ABF\backsim\triangle CBE$；
（2）如图2，连接$AE$，点$P$，$M$，$N$分别为线段$AC$，$AE$，$EF$的中点，连接$PM$，$MN$，$PN$.求$\angle PMN$的度数及$\frac{MN}{PM}$的值；
（3）在（2）的条件下，若$BC=\sqrt{2}$，直接写出$\triangle PMN$面积的最大值.

答案：
［解析］（1）如图1，$\because CA = CB$，$\angle ACB = 90^{\circ}$，$EF = EB$，$\angle BEF = 90^{\circ}$，$\therefore\angle CBA=\angle EBF = 45^{\circ}$，$AB=\sqrt{2}BC$，$BF=\sqrt{2}BE$，$\therefore\angle CBE=\angle ABF$，$\frac{AB}{BC}=\frac{BF}{BE}=\sqrt{2}$，$\therefore\triangle ABF\sim\triangle CBE$；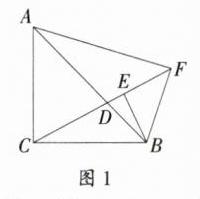
（2）如图2，延长$PM$交$AF$于$T$。$\because BE\perp CF$，$\therefore\angle CEB = 90^{\circ}$，$\because\triangle ABF\sim\triangle CBE$，$\therefore\angle CEB=\angle AFB = 90^{\circ}$，$\frac{AF}{EC}=\frac{AB}{BC}=\sqrt{2}$，$\therefore AF=\sqrt{2}EC$，$\because\angle EFB = 45^{\circ}$，$\therefore\angle AFC = 45^{\circ}$，$\because AP = PC$，$AM = ME$，$\therefore PT\parallel CF$，$PM=\frac{1}{2}EC$，$\because AM = ME$，$EN = NF$，$\therefore MN\parallel AF$，$MN=\frac{1}{2}AF$，$\therefore$四边形$MNFT$是平行四边形，$MN=\sqrt{2}PM$，$\therefore\angle TMN=\angle AFC = 45^{\circ}$，$\therefore\angle PMN = 135^{\circ}$，$\therefore\frac{MN}{PM}=\sqrt{2}$；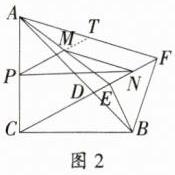
 （3）$\triangle PMN$面积的最大值为$\frac{1}{2}$。提示：$\because MN=\sqrt{2}PM$，$\angle PMN = 135^{\circ}$，$PM=\frac{1}{2}EC$，$\therefore$当$EC$的值最大时，$PM$的值最大，此时$\triangle PMN$的面积最大，$\because$当点$E$与$B$重合时，$EC$的值最大，$EC$的最大值为$\sqrt{2}$，此时$PM=\frac{\sqrt{2}}{2}$，$MN=\sqrt{2}PM = 1$，$\therefore\triangle PMN$的面积的最大值为$\frac{1}{2}\times\frac{\sqrt{2}}{2}\times1\times\frac{\sqrt{2}}{2}=\frac{1}{4}$。