《2025年考点集训与满分备考九年级数学全一册下人教版》

1. 在$\triangle ABC$中，$\angle A = 60^{\circ}$，$AB = 6\ cm$，$AC = 4\ cm$，则$\triangle ABC$的面积是（ ）
A. $2\sqrt{3}\ cm^{2}$
B. $4\sqrt{3}\ cm^{2}$
C. $6\sqrt{3}\ cm^{2}$
D. $12\ cm^{2}$

答案：
C　[解析]如图，过点C作高CD.
∵∠A=60°,AC=4cm,
∴CD=AC·sin60° = 2$\sqrt{3}$cm.
∴△ABC的面积为$\frac{1}{2}$CD×AB = 6$\sqrt{3}$cm²
　　　

2. 设$a$，$b$，$c$分别为$\triangle ABC$中$\angle A$，$\angle B$和$\angle C$的对边，则下列不能表示$\triangle ABC$的面积的是（ ）
A. $\frac{1}{2}ab\sin C$
B. $\frac{1}{2}ac\sin B$
C. $\frac{1}{2}cb\sin A$
D. $\frac{1}{2}ab\sin A$

答案：
D　[解析]如图,过点A作BC边上的高AD,则Rt△ACD中,
AD = AC·sinC = bsinC,
∴△ABC的面积为$\frac{1}{2}$absinC;
　同理,S_{△ABC}=$\frac{1}{2}$acsinB = $\frac{1}{2}$cbsinA.
　　　　

3. [广东湛江霞山区期末]在$\triangle ABC$中，若$AB = 6$，$BC = 8$，$\angle B = 120^{\circ}$，则$\triangle ABC$的面积为________.

答案：
12$\sqrt{3}$　[解析]如图,过点A作AD⊥BC,交CB延长线于点D,
∵∠ABC = 120°,
∴∠ABD = 180° - 120° = 60°，
∵sin∠ABD = $\frac{AD}{AB}$，
∴AD = AB·sin∠ABD = 6×$\frac{\sqrt{3}}{2}$ = 3$\sqrt{3}$，
∴△ABC的面积 = $\frac{1}{2}$BC·AD = $\frac{1}{2}$×8×3$\sqrt{3}$ = 12$\sqrt{3}$.
　　　

4. [安徽安庆潜山期末]如图，$\triangle ABC$中，过点$B$作$BD\perp AB$，交$AC$于点$D$，且$AD:CD = 4:3$，$\angle ABC = 150^{\circ}$.
（1）$BD:BC = $________；
（2）若$AB = 4$，则$\triangle ABC$的面积是________.

答案：

(1)2:7　
(2)2$\sqrt{3}$　[解析]
(1)如图,过点C作CE⊥AB,交AB的延长线于点E，
∵∠ABC = 150°，
∴∠CBE = 180° - ∠ABC = 30°，
∴设CE = a(a＞0)，则BC = 2a，
∵BD⊥AB，CE⊥AB，
∴∠ABD = ∠AEC = 90°，
∵∠A = ∠A，
∴△ABD∽△AEC，
∴$\frac{AD}{AC}$ = $\frac{BD}{CE}$，
∴$\frac{4}{7}$ = $\frac{BD}{a}$，
∴BD = $\frac{4}{7}$a，
∴$\frac{BD}{BC}$ = $\frac{\frac{4}{7}a}{2a}$ = $\frac{2}{7}$；
(2)由
(1)得△ABD∽△AEC，
∴$\frac{AD}{AC}$ = $\frac{AB}{AE}$，
∴$\frac{4}{7}$ = $\frac{4}{AE}$，
∴AE = 7，
∴BE = AE - AB = 7 - 4 = 3，
　在Rt△BEC中，
　CE = BE·tan30° = 3×$\frac{\sqrt{3}}{3}$ = $\sqrt{3}$，
∴△ABC的面积 = $\frac{1}{2}$AB·CE = $\frac{1}{2}$×4×$\sqrt{3}$ = 2$\sqrt{3}$.
　　

5. [湖北恩施州鹤峰模拟]在某高速公路建设过程中，途经如图某处山峰时，施工方案选择了沿直线$AB$开凿穿山隧道，山顶有一铁塔$EF$，塔高$35\ m$，从与点$C$相距$60\ m$的点$A$测得$E$，$F$的仰角分别为$34.97^{\circ}$，$38.53^{\circ}$，从与点$D$相距$50\ m$的点$B$测得$F$的仰角为$45^{\circ}$，求隧道$CD$的长度.(参考数据：$\tan34.97^{\circ}\approx0.70$，$\tan38.53^{\circ}\approx0.80$)

答案：
[解析]如图,过点E作EG⊥AB于点G,由题意可知,E,F,G在同一直线上,在Rt△AGF中,GF = AGtan38.53°,在Rt△AGE中,GE = AG·tan34.97°,
∴EF = GF - GE = AG·tan38.53° - AG·tan34.97°,
∴AG = $\frac{EF}{tan38.53° - tan34.97°}$≈350m,在Rt△BGF中,
∵∠B = 45°,
∴BG = GF = AG·tan38.53°≈350×0.8 = 280(m),
∴隧道CD = AG + BG - AC - BD = 350 + 280 - 60 - 50 = 520(m),
　即隧道CD的长度为520m.
　　

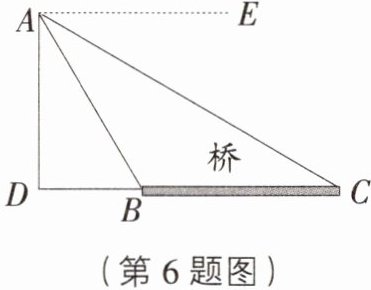
6. [河北石家庄长安区二模]如图，嘉琪在一座桥的附近试飞一架小型无人机，无人机飞行的高度为$AD$，且$D$，$B$，$C$在同一水平线上.
（1）有下列说法：①无人机俯视桥头$B$的俯角为$\angle EAC$；②无人机俯视桥头$C$的俯角为$\angle C$；③站在桥头$B$处看无人机的仰角为$\angle ABD$；④从$C$处走向$B$处的过程中观察无人机，仰角越来越大；其中正确的是________（只填序号即可）；
（2）若$\angle EAB = 60^{\circ}$，$\angle EAC = 30^{\circ}$，桥$BC$的长度为$24\ m$，求无人机的飞行高度$AD$.（结果精确到$1\ m$，参考数据：$\sqrt{3}\approx1.73$）

答案： [解析]
(1)③④　提示:①无人机俯视桥头B的俯角为∠EAB,故①不正确;②无人机俯视桥头C的俯角为∠CAE,故②不正确;③站在桥头B 处看无人机的仰角为∠ABD,故③正确;④从C处走向B处的过程中观察无人机，仰角越来越大,故④正确;
(2)
∵∠EAB = 60°,∠EAC = 30°,
∴∠CAD = 60°,∠BAD = 30°,
∴CD = AD·tan∠CAD = $\sqrt{3}$AD,
BD = AD·tan∠BAD = $\frac{\sqrt{3}}{3}$AD,
∴BC = CD - BD = $\frac{2\sqrt{3}}{3}$AD = 24m,解得AD = 12$\sqrt{3}$≈21(m).即无人机的飞行高度AD约为21m.