《2025年考点集训与满分备考九年级数学全一册下人教版》

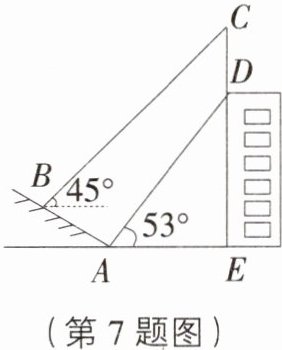
7. [广东中山一模]如图，某大楼的顶部竖有一块广告牌$CD$，小马同学在山坡的坡脚$A$处测得广告牌底部$D$的仰角为$53^{\circ}$，沿坡面$AB$向上走到$B$处测得广告牌顶部$C$的仰角为$45^{\circ}$，已知山坡$AB$的坡比$i = 1:\sqrt{3}$，$AB = 10\ m$，$AE = 21\ m$.测角器的高度忽略不计，参考数据：$\sqrt{2}\approx1.41$，$\sqrt{3}\approx1.73$，$\sin53^{\circ}\approx\frac{4}{5}$，$\cos53^{\circ}\approx\frac{3}{5}$，$\tan53^{\circ}\approx\frac{4}{3}$
（1）求点$B$距水平地面$AE$的高度；
（2）若市政规定广告牌的高度不得大于$7\ m$，请问该公司的广告牌是否符合要求，并说明理由.

答案：
[解析]
(1)如图,过点B作BM⊥AE,BN⊥CE,垂足分别为M,N.由题意可知∠CBN = 45°,∠DAE = 53°,
　i = 1:$\sqrt{3}$,AB = 10m,AE = 21m.
∵i = 1:$\sqrt{3}$ = $\frac{BM}{AM}$ = tan∠BAM,
∴∠BAM = 30°,
∴BM = $\frac{1}{2}$AB = 5m,即点B距水平地面AE的高度为5m.
　　
(2)由
(1)知BM = 5m,∠BAM = 30°,在Rt△ABM中,AM = $\frac{\sqrt{3}}{2}$AB = 5$\sqrt{3}$m,
∴ME = AM + AE = (5$\sqrt{3}$ + 21)m = BN,
∵∠CBN = 45°,
∴CN = BN = ME = (5$\sqrt{3}$ + 21)m,
∴CE = CN + NE = (5$\sqrt{3}$ + 26)m,
　在Rt△ADE中,
　∠DAE = 53°,AE = 21m,
∴DE = AE·tan53°≈21×$\frac{4}{3}$ = 28,
∴CD = CE - DE = 5$\sqrt{3}$ + 26 - 28 = 5$\sqrt{3}$ - 2≈6.7(m)＜7m,
∴符合要求.

8. [安徽宣城模拟]我们知道，直角三角形的边角关系可用三角函数来描述，那么在任意三角形中，边角之间是否也存在某种关系呢?
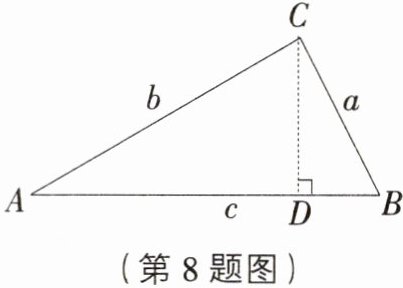
如图，锐角三角形$ABC$中，$\angle A$，$\angle B$，$\angle C$所对的边分别为$a$，$b$，$c$，过点$C$作$CD\perp AB$，在$Rt\triangle ADC$中，$CD = b\sin A$，$AD = b\cos A$，$\therefore BD = c - b\cos A$，
在$Rt\triangle BDC$中，由勾股定理，
得$BD^{2}+CD^{2}=BC^{2}$，
即$(c - b\cos A)^{2}+(b\sin A)^{2}=a^{2}$，
整理可得$a^{2}=b^{2}+c^{2}-2bc\cos A$，
同理可得$b^{2}=a^{2}+c^{2}-2ac\cos B$，$c^{2}=a^{2}+b^{2}-2ab\cos C$.
利用上述结论解答下列问题：
（1）在$\triangle ABC$中，$\angle A = 45^{\circ}$，$b = 2\sqrt{2}$，$c = 2$，求$a$和$\angle C$的大小；
（2）在$\triangle ABC$中，$a = \sqrt{3}$，$b = \sqrt{2}$，$\angle B = 45^{\circ}$，且$c ＞ a ＞ b$，求边长$c$的长度.

答案： [解析]
(1)在△ABC中,a² = b² + c² - 2bc cosA = (2$\sqrt{2}$)² + 2² - 2×2$\sqrt{2}$×2×$\frac{\sqrt{2}}{2}$ = 4,
∴a = 2.
∵2² + 2² = (2$\sqrt{2}$)²,即a² + c² = b²,
∴△ABC为直角三角形，∠B = 90°.又
∵∠A = 45°,
∴∠C = 45°;
(2)
∵b² = a² + c² - 2accosB,a = $\sqrt{3}$,b = $\sqrt{2}$,∠B = 45°,
∴($\sqrt{2}$)² = ($\sqrt{3}$)² + c² - 2$\sqrt{3}$c·cos45°,化简得c² - $\sqrt{6}$c + 1 = 0,解得c = $\frac{\sqrt{6} \pm \sqrt{2}}{2}$.
∵c ＞ a ＞ b,
∴c = $\frac{\sqrt{6} + \sqrt{2}}{2}$.