《2025年考点集训与满分备考九年级数学全一册下人教版》

13. [河南郑州期末]如图，已知Rt△ABC中，∠ACB=90°，AC:AB=3:5，则tanA的值为（ ）
A. $\frac{3}{5}$
B. $\frac{4}{3}$
C. $\frac{3}{4}$
D. $\frac{4}{5}$

答案： B [解析]
∵∠ACB = 90°，AC:AB = 3:5，设AC = 3x(x＞0)，则AB = 5x，
∴BC = $\sqrt{AB^{2}-AC^{2}}$ = $\sqrt{(5x)^{2}-(3x)^{2}}$ = 4x，
∴tan A = $\frac{BC}{AC}$ = $\frac{4x}{3x}$ = $\frac{4}{3}$。

14. 难点[上海浦东新区期末]如图，在平面直角坐标系xOy中，点P的坐标为(3，4)，射线OP与x轴的正半轴所夹的角为α，那么α的余弦值等于________.

答案：
$\frac{3}{5}$ [解析]如图，过P作PA⊥x轴于点A，
∵P(3,4)，
∴PA = 4，OA = 3，由勾股定理，得OP = 5，
∴α的余弦值是$\frac{OA}{OP}$ = $\frac{3}{5}$。

15. [陕西韩城期末]如图，在Rt△ABC中，∠C=90°，AC=12，BC=5.求sinA，cosA和tanA.

答案： [解析]在Rt△ABC中，∠C = 90°，AC = 12，BC = 5。
∴AB = $\sqrt{AC^{2}+BC^{2}}$ = $\sqrt{12^{2}+5^{2}}$ = 13，
∴sin A = $\frac{BC}{AB}$ = $\frac{5}{13}$，cos A = $\frac{AC}{AB}$ = $\frac{12}{13}$，tan A = $\frac{BC}{AC}$ = $\frac{5}{12}$。

16. [浙江杭州中考]如图，在△ABC中，∠C=90°，设∠A，∠B，∠C所对的边分别为a，b，c，则（ ）


A. c=bsinB
B. b=csinB
C. a=btanB
D. b=ctanB

答案： B [解析]
∵在△ABC中，∠C = 90°，∠A，∠B，∠C所对的边分别为a，b，c，
∴sin B = $\frac{b}{c}$，即b = csin B，故A选项不成立，B选项成立；tan B = $\frac{b}{a}$，即b = atan B，故C选项不成立，D选项也不成立。

17. [云南中考]在Rt△ABC中，∠C=90°，AC=1，BC=3，则∠A的正切值为（ ）
A. 3
B. $\frac{1}{3}$
C. $\frac{\sqrt{10}}{10}$
D. $\frac{3\sqrt{10}}{10}$

答案： A [解析]
∵在Rt△ABC中，∠C = 90°，AC = 1，BC = 3，
∴∠A的正切值为$\frac{BC}{AC}$ = $\frac{3}{1}$ = 3。

18. [湖北宜昌中考]如图，△ABC的顶点是正方形网格的格点，则cos∠ABC的值为（ ）
A. $\frac{\sqrt{2}}{3}$
B. $\frac{\sqrt{2}}{2}$
C. $\frac{4}{3}$
D. $\frac{2\sqrt{2}}{3}$

答案：
B [解析]如图，在Rt△ABD中，∠ADB = 90°，AD = BD = 3，
∴AB = $\sqrt{AD^{2}+BD^{2}}$ = $\sqrt{3^{2}+3^{2}}$ = 3$\sqrt{2}$，
∴cos∠ABC = $\frac{BD}{AB}$ = $\frac{3}{3\sqrt{2}}$ = $\frac{\sqrt{2}}{2}$。

19. [广西桂林中考]如图，在Rt△ABC中，∠C=90°，AB=13，AC=5，则cosA的值是__________.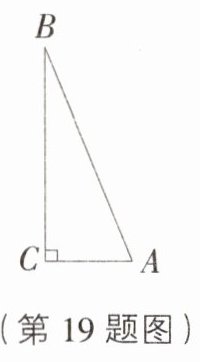

答案： $\frac{5}{13}$ [解析]在Rt△ABC中，cos A = $\frac{AC}{AB}$ = $\frac{5}{13}$。

20. [云南西双版纳景洪一中期末]如图，在Rt△ABC中，∠C=90°，BC=1，AC=2.
(1)求sinA，sinB，cosA，cosB的值；
(2)通过计算你有什么发现？请加以说明.

答案： [解析]
(1)在Rt△ABC中，
∵∠C = 90°，
∴AB = $\sqrt{AC^{2}+BC^{2}}$ = $\sqrt{2^{2}+1^{2}}$ = $\sqrt{5}$，
∴sin A = $\frac{BC}{AB}$ = $\frac{1}{\sqrt{5}}$ = $\frac{\sqrt{5}}{5}$，sin B = $\frac{AC}{AB}$ = $\frac{2}{\sqrt{5}}$ = $\frac{2\sqrt{5}}{5}$，cos A = $\frac{AC}{AB}$ = $\frac{2}{\sqrt{5}}$ = $\frac{2\sqrt{5}}{5}$，cos B = $\frac{BC}{AB}$ = $\frac{1}{\sqrt{5}}$ = $\frac{\sqrt{5}}{5}$；
(2)发现：互余两角的正弦、余弦之间存在以下关系：若∠A + ∠B = 90°，则sin A = cos B，sin B = cos A。
说明：在Rt△ABC中，∠C = 90°，设BC = a，AC = b，AB = c，则sin A = $\frac{a}{c}$，cos B = $\frac{a}{c}$，sin B = $\frac{b}{c}$，cos A = $\frac{b}{c}$，
∴sin A = cos B，sin B = cos A。