《2025年考点集训与满分备考九年级数学全一册下人教版》

1. [安徽蚌埠二模]如图,点$P$是$x$轴正半轴上的一个动点,过点$P$作$PQ\perp x$轴交双曲线$y = \frac{3}{x}$($x＞0$)于点$Q$,连接$OQ$,当点$P$沿$x$轴的正方向运动时,$Rt\triangle QOP$的面积 ( )

A. 保持不变
B. 逐渐减少
C. 逐渐增大
D. 无法确定

答案： A [解析]因为过双曲线上任意一点与原点所连的线段、坐标轴、过该点向坐标轴所作的垂线所围成的直角三角形的面积 S 是个定值，即$S = \frac{1}{2}|k|$.$\because PQ\perp x$轴，点 Q 在双曲线$y = \frac{3}{x}(x ＞ 0)$上，$\therefore S_{\triangle OQP}=\frac{3}{2}$.

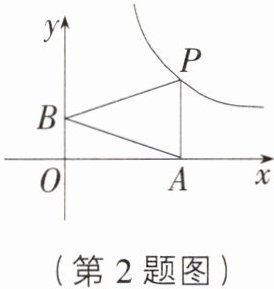
2. [河北唐山路南区二模]如图,已知动点$A$,$B$分别在$x$轴,$y$轴正半轴上,动点$P$在反比例函数$y = \frac{1}{x}$($x＞0$)图象上,$PA\perp x$轴,当点$A$的横坐标逐渐增大时,$\triangle PAB$的面积将会 ( )

A. 越来越小
B. 越来越大
C. 不变
D. 先变大后变小

答案：
C [解析]如图，过点 B 作$BC\perp PA$于点 C，则$BC = OA$，设点$P(x,\frac{1}{x})(x ＞ 0)$，则$S_{\triangle PAB}=\frac{1}{2}PA\cdot BC=\frac{1}{2}\cdot\frac{1}{x}\cdot x=\frac{1}{2}$，当点 A 的横坐标逐渐增大时，$S_{\triangle PAB}$不变，始终等于$\frac{1}{2}$.
　　　

3. [湖南长沙雨花区模拟]如图,在平面直角坐标系中,第二象限内的点$P$是反比例函数$y = \frac{k}{x}$($k\ne0$)图象上的一点,过点$P$作$PA\perp x$轴于点$A$,点$B$为$AO$的中点,若$\triangle PAB$的面积为$3$,则$k$的值为 ________.

答案： -12 [解析]在题图上连接 OP.$\because$点 B 为 AO 的中点，$\triangle PAB$的面积为 3，$\therefore S_{\triangle OAP}=2S_{\triangle PAB}=2\times3 = 6$，又$\because S_{\triangle OAP}=\frac{1}{2}|k|$，$\therefore\frac{1}{2}|k| = 6$，$\therefore|k| = 12$，$\because$图象位于第二象限，$\therefore k ＜ 0$，$\therefore k = -12$.

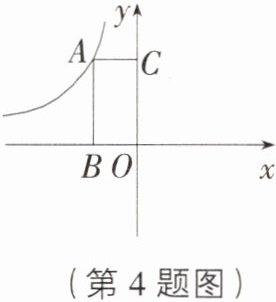
4. [甘肃庆阳中考]如图,矩形$ABOC$的面积为$3$,反比例函数$y = \frac{k}{x}$的图象过点$A$,则$k$等于 ( )

A. 3
B. -1.5
C. -6
D. -3

答案： D [解析]依题意，有$|k| = 3$，$\therefore k = \pm3$，又$\because$图象位于第二象限，$\therefore k ＜ 0$，$\therefore k = -3$.

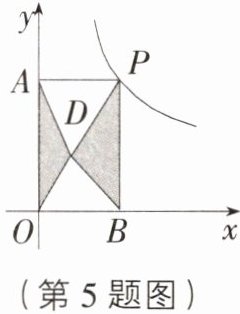
5. [山西临汾期末]如图,点$P$是反比例函数$y = \frac{6}{x}$($x＞0$)的图象上的任意一点,过点$P$分别作两坐标轴的垂线,垂足分别为点$B$,$A$,与坐标轴构成矩形$OAPB$,点$D$是矩形$OAPB$内任意一点,连接$DA$,$DB$,$DP$,$DO$,则图中阴影部分的面积是 ( )

A. 1
B. 2
C. 3
D. 4

答案： C [解析]$\because$点 P 是反比例函数$y = \frac{6}{x}(x ＞ 0)$的图象上的任意一点，过点 P 分别作两坐标轴的垂线，$\therefore$矩形 OAPB 的面积为 6.$\therefore$阴影部分的面积$=\frac{1}{2}\times$矩形 OAPB 的面积 = 3.

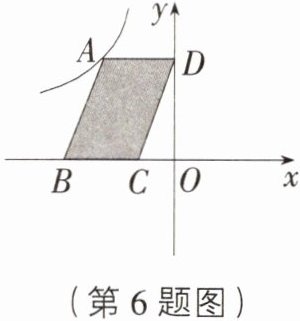
6. [江苏无锡期中]如图,点$A$是反比例函数$y = \frac{k}{x}$($x＜0$)的图象上的一点,过点$A$作平行四边形$ABCD$,使点$B$,$C$在$x$轴上,点$D$在$y$轴上.已知平行四边形$ABCD$的面积为$8$,则$k$的值为 ( )

A. 8
B. -8
C. 4
D. -4

答案：
B [解析]如图，作$AE\perp BC$于点 E，$\because$四边形 ABCD 为平行四边形，$\therefore AD// x$轴，$\therefore$四边形 ADOE 为矩形，$\therefore S_{平行四边形 ABCD}=S_{矩形 ADOE}$，而$S_{矩形 ADOE}=|k|$，$\therefore|k| = 8$，又$\because$图象位于第二象限，$\therefore k ＜ 0$，$\therefore k = -8$.