《2025年考点集训与满分备考九年级数学全一册下人教版》

17. [山东潍城期中]如图，∠α的顶点位于正方形网格的格点上，若tanα=$\frac{1}{2}$，则满足条件的是______.(填序号)

答案：
①④　[解析]①观察图形可得$\tan\alpha=\frac{1}{2}$，符合题意；②观察图形可得$\tan\alpha = 1$，不符合题意；③观察图形可得$\tan\alpha = 2$，不符合题意；④如图,延长BC至D，连接AD，则∠ADB = 90°，设小正方形的边长为1，则AD = $\sqrt{1^{2}+1^{2}}=\sqrt{2}$，BD = $\sqrt{2^{2}+2^{2}}=2\sqrt{2}$，
∴$\tan\alpha=\frac{AD}{BD}=\frac{\sqrt{2}}{2\sqrt{2}}=\frac{1}{2}$，符合题意。

18. [北京西城区期中]如图，在△ABC中，∠B=30°，∠BAC=105°，AB=6，则∠C=_______，BC的长是_______.

答案：
45° $3\sqrt{3}+3$［解析］如图，过点A作AD⊥BC于点D.
∵∠B = 30°，AB = 6，
∴AD = $\frac{1}{2}AB = 3$，∠BAD = 90° - 30° = 60°，BD = AB·$\cos30^{\circ}=6×\frac{\sqrt{3}}{2}=3\sqrt{3}$，
∵∠BAC = 105°，
∴∠CAD = 105° - 60° = 45°，
∴△ACD是等腰直角三角形，
∴CD = AD = 3，∠C = 45°，
∴BC = BD + CD = 3$\sqrt{3}+3$。

19. [湖北随州中考]如图，某梯子长10 m，斜靠在竖直的墙面上，当梯子与水平地面所成角为α时，梯子顶端靠在墙面上的点A处，底端落在水平地面的点B处，现将梯子底端向墙面靠近，使梯子与水平地面所成角为β，已知sinα=cosβ=$\frac{3}{5}$，则梯子顶端上升了__________ m.

答案：
2　[解析]如图,在Rt△ABC中,AC = AB·$\sin\alpha = 10×\frac{3}{5}=6$(m)；在Rt△DEC中，DC = DE·$\cos\beta = 10×\frac{3}{5}=6$(m)，EC = $\sqrt{DE^{2}-DC^{2}}=\sqrt{100 - 36}=8$(m)；
∴AE = EC - AC = 8 - 6 = 2(m)。

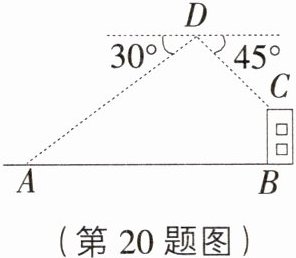
20. [湖南永州宁远模拟]如图，某无人机兴趣小组在操场上开展活动，此时无人机在离地面20$\sqrt{3}$ m的D处，无人机测得操控者A的俯角为30°，测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC之间的水平距离为80 m，则教学楼BC的高度约为________ m.(注：点A，B，C，D都在同一平面上，参考数据：$\sqrt{3}$≈1.7，结果保留整数)

答案： 14　[解析]在题图上过点D作DE⊥AB于点E，过点C作CF⊥DE于点F，则四边形BCFE是矩形.由题意，得AB = 80 m，DE = 20$\sqrt{3}$m，∠ADE = 90° - 30° = 60°，∠CDF = 90° - 45° = 45°.在Rt△ADE中，∠AED = 90°，
∵$\tan\angle ADE=\frac{AE}{DE}=\tan60^{\circ}=\sqrt{3}$，
∴AE = $\sqrt{3}DE = 60$m，
∴BE = AB - AE = 80 - 60 = 20(m)，
∵四边形BCFE是矩形，
∴CF = BE = 20 m，在Rt△DCF中，∠DFC = 90°，∠CDF = ∠DCF = 45°，
∴DF = CF = 20 m，
∴BC = EF = DE - DF = 20$\sqrt{3}-20\approx14$(m)。

21. (6分)计算：
(1)2sin30°+3cos60°-4tan45°；
(2)[山东济南任城区月考]tan60°-(4-π)⁰+2cos30°+|$\frac{1}{4}$|⁻¹.

答案： [解析]
(1)原式 = 2×$\frac{1}{2}+3×\frac{1}{2}-4×1 = 1+\frac{3}{2}-4=-\frac{3}{2}$；
(2)原式 = $\sqrt{3}-1+2×\frac{\sqrt{3}}{2}+4=\sqrt{3}-1+\sqrt{3}+4=2\sqrt{3}+3$。

22. (8分)[安徽模拟]如图，在Rt△ABC中，∠C=90°，D为BC的中点，AB=5，AC=3.
(1)求AD的长；
(2)求sin∠DAB的值.

答案：
[解析]
(1)
∵∠C = 90°，AB = 5，AC = 3，
∴BC = $\sqrt{AB^{2}-AC^{2}}=\sqrt{5^{2}-3^{2}} = 4$。
∵D是BC的中点，
∴CD = $\frac{1}{2}BC = 2$。
∴AD = $\sqrt{AC^{2}+CD^{2}}=\sqrt{3^{2}+2^{2}}=\sqrt{13}$；
(2)过点D作DE⊥AB，垂足为点E.
∵D为BC的中点，
∴$S_{\triangle ACD}=S_{\triangle ADB}=\frac{1}{2}AC×CD = 3$。
∵$S_{\triangle ABD}=\frac{1}{2}AB×DE = 3$，
∴DE = $\frac{6}{5}$。
∴$\sin\angle DAB=\frac{DE}{AD}=\frac{\frac{6}{5}}{\sqrt{13}}=\frac{6\sqrt{13}}{65}$。

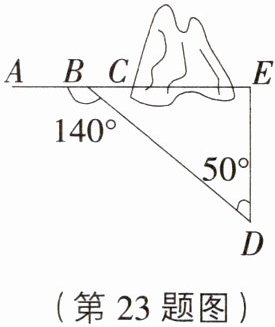
23. (8分)[湖北宜昌五峰模拟]某市将推进轨道交通一号线的建设.如图，工程队拟沿AC方向开山修路，为加快施工进度，需在小山的另一边的点E处同时施工.要使A，C，E三点在一条直线上，工程队从AC上的一点B取∠ABD=140°，BD=560 m，∠D=50°.那么点E与点D间的距离是多少米？(参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19)

答案： [解析]
∵A，C，E三点在一条直线上，∠ABD = 140°，∠D = 50°，
∴∠E = ∠ABD - ∠D = 140° - 50° = 90°，在Rt△BDE中，BD = 560 m，
∴DE = BD·$\cos D = 560×\cos50^{\circ}\approx560×0.64 = 358.4$(m)，即点E与点D间的距离是358.4 m。