《2025年考点集训与满分备考九年级数学全一册下人教版》

1. 如图，一艘海轮位于灯塔P的南偏东37°方向，距离灯塔40 n mile的A处，它沿正北方向航行一段时间后，到达位于灯塔的正东方向上的B处，这时，B处与灯塔P的距离PB的长可以表示为 ( )

A. 40 n mile
B. 40sin37° n mile
C. 40cos37° n mile
D. 40tan37° n mile

答案： B　[解析]
∵一艘海轮位于灯塔P 的南偏东37°方向，
∴∠BAP = 37°，
∵AP = 40n mile，
∴BP = AP·sin37° = 40sin37°n mile。

2. 如图，一艘客轮从小岛A沿东北方向航行，同时一艘补给船从小岛A正东方向相距(100 + 100$\sqrt{3}$) n mile的港口B出发，沿北偏西60°方向航行，与客轮同时到达C处给客轮进行补给，则客轮与补给船的速度之比为 ( )

A. $\sqrt{2}$:2
B. $\sqrt{2}$:1
C. $\sqrt{3}$:2
D. $\sqrt{3}$:1

答案：
A　[解析]过点C作CD⊥AB于点D，如图，设AD = xn mile，由题意得∠CAD = 45°，∠NBC = 60°，在Rt△ACD中，∠ACD = 90° - 45° = 45°，
∴∠ACD = ∠CAD，
∴CD = AD = xn mile，
∴AC = $\sqrt{CD^{2}+AD^{2}}$ = $\sqrt{2}$xn mile，在Rt△BCD中，∠CBD = 90° - 60° = 30°，
∴BC = 2CD = 2xn mile，
∴BD = $\sqrt{BC^{2}-CD^{2}}$ = $\sqrt{3}$xn mile，
∵AB = AD + BD = (100 + 100$\sqrt{3}$)n mile，
∴x + $\sqrt{3}$x = 100(1 + $\sqrt{3}$)，
∴x = 100，即AD = 100n mile，
∴AC = 100$\sqrt{2}$n mile，BC = 200n mile，
∵时间一定时速度与路程成正比，
∴客轮与补给船的速度之比为100$\sqrt{2}$:200 = $\sqrt{2}$:2。

3. 一名徒步爱好者来某地旅行，他从宾馆C处出发，沿北偏东30°的方向行走2 000 m到达某书院A处，参观后又从A处沿正南方向行走一段距离，到达位于宾馆C处南偏东45°方向的滨江公园B处，如图所示，则AB的距离为 ____________ m.

答案：
(1000$\sqrt{3}$ + 1000)　[解析]过点C作CP⊥AB于点P，如图，则∠APC = ∠BPC = 90°。由题意，可得∠A = 30°，AC = 2000m，∠BCP = 45°，
∴PC = $\frac{1}{2}$AC = 1000m，
∴AP = AC·cos30° = 1000$\sqrt{3}$m，在Rt△PBC中，PC = 1000m，∠BCP = 45°，
∴△BCP是等腰直角三角形，
∴BP = PC = 1000m，
∴AB = AP + BP = (1000$\sqrt{3}$ + 1000)m。

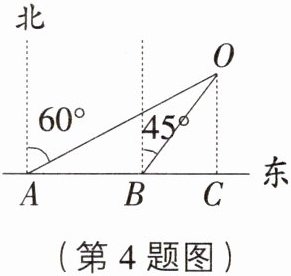
4. 如图，某船由西向东航行，在点A处测得小岛O在北偏东60°方向上，船航行了10 n mile后到达点B.这时测得小岛O在北偏东45°方向上，船继续航行到点C时，测得小岛O恰好在船的正北方，求此时船到小岛的距离. (结果保留根号)

答案： [解析]设OC = xn mile，依题意，得∠OAB = 30°，∠OBC = ∠BOC = 45°，
∵OC⊥AB，
∴BC = OC = xn mile，AC = $\sqrt{3}$xn mile，
∵AB = 10n mile，
∴$\sqrt{3}$x - x = 10，解得x = 5($\sqrt{3}$ + 1)，即船与小岛的距离是5($\sqrt{3}$ + 1)n mile。

5. 堤的横断面如图.堤高BC是5 m，迎水斜坡AB的长是13 m，那么斜坡AB的坡度是 ( )

A. 1:3
B. 1:2.6
C. 1:2.4
D. 1:2

答案： 5.C　[解析]由勾股定理，得AC = 12m。则斜坡AB的坡度为BC:AC = 5:12 = 1:2.4。

6. 如图，在坡角为α的山坡上栽树，要求相邻两树之间的水平距离为6 m，那么相邻两树在坡面上的距离AB为 ( )

A. 6cosα m
B. $\frac{6}{\cos\alpha}$ m
C. 6sinα m
D. $\frac{6}{\sin\alpha}$ m

答案：
B　[解析]如图，在Rt△ABC中，BC = 6m，∠ABC = α，
∵cos∠ABC = $\frac{BC}{AB}$，
∴AB = $\frac{BC}{cos∠ABC}$ = $\frac{6}{cosα}$m。