第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
9. [浙江杭州模拟]在Rt△ABC中,∠C = 90°,AC:BC = 1:2,则∠A的正弦值为 ( )
A. $\frac{\sqrt{5}}{5}$
B. $\frac{2\sqrt{5}}{5}$
C. 2
D. $\frac{\sqrt{5}}{2}$
A. $\frac{\sqrt{5}}{5}$
B. $\frac{2\sqrt{5}}{5}$
C. 2
D. $\frac{\sqrt{5}}{2}$
答案:
B [解析]设AC = x(x>0),则BC = 2x,由勾股定理得$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{5}x$,
∴$\sin A=\frac{BC}{AB}=\frac{2x}{\sqrt{5}x}=\frac{2\sqrt{5}}{5}$。
∴$\sin A=\frac{BC}{AB}=\frac{2x}{\sqrt{5}x}=\frac{2\sqrt{5}}{5}$。
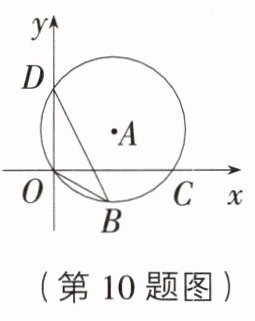
10. [河南驻马店新蔡模拟]如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD = ( )
A. $\frac{1}{2}$
B. $\frac{3}{4}$
C. $\frac{4}{5}$
D. $\frac{3}{5}$

A. $\frac{1}{2}$
B. $\frac{3}{4}$
C. $\frac{4}{5}$
D. $\frac{3}{5}$
答案:
D [解析]在题图上连接CD,
∵D(0,3),C(4,0),
∴OD = 3,OC = 4,
∵∠COD = 90°,
∴$CD=\sqrt{3^{2}+4^{2}} = 5$,
∵∠OBD = ∠OCD,
∴$\sin\angle OBD=\sin\angle OCD=\frac{OD}{CD}=\frac{3}{5}$。
∵D(0,3),C(4,0),
∴OD = 3,OC = 4,
∵∠COD = 90°,
∴$CD=\sqrt{3^{2}+4^{2}} = 5$,
∵∠OBD = ∠OCD,
∴$\sin\angle OBD=\sin\angle OCD=\frac{OD}{CD}=\frac{3}{5}$。
11. [四川达州渠县崇德实验学校模拟]如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD = 2,AC = 3,则sinB的值是______.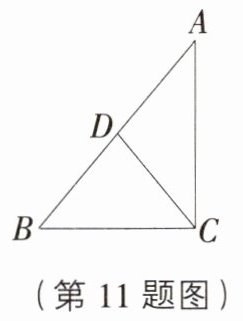

答案:
$\frac{3}{4}$ [解析]
∵在Rt△ABC中,CD是斜边AB上的中线,CD = 2,
∴AB = 2CD = 4,则$\sin B=\frac{AC}{AB}=\frac{3}{4}$。
∵在Rt△ABC中,CD是斜边AB上的中线,CD = 2,
∴AB = 2CD = 4,则$\sin B=\frac{AC}{AB}=\frac{3}{4}$。
12. 难点[北京门头沟区模拟]如图,A,B,C是小正方形的顶点,且每个小正方形的边长相同,那么∠BAC的正弦值为________.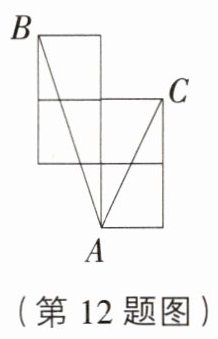

答案:
$\frac{\sqrt{2}}{2}$ [解析]连接BC,如图.设小正方形的边长为1,
∵$CB=\sqrt{1^{2}+2^{2}}=\sqrt{5}$,$AC=\sqrt{1^{2}+2^{2}}=\sqrt{5}$,$AB=\sqrt{1^{2}+3^{2}}=\sqrt{10}$,
∴$CB^{2}+CA^{2}=AB^{2}$,
∴△ACB为直角三角形,∠ACB = 90°,
∴$\sin\angle BAC=\frac{BC}{AB}=\frac{\sqrt{5}}{\sqrt{10}}=\frac{\sqrt{2}}{2}$。

$\frac{\sqrt{2}}{2}$ [解析]连接BC,如图.设小正方形的边长为1,
∵$CB=\sqrt{1^{2}+2^{2}}=\sqrt{5}$,$AC=\sqrt{1^{2}+2^{2}}=\sqrt{5}$,$AB=\sqrt{1^{2}+3^{2}}=\sqrt{10}$,
∴$CB^{2}+CA^{2}=AB^{2}$,
∴△ACB为直角三角形,∠ACB = 90°,
∴$\sin\angle BAC=\frac{BC}{AB}=\frac{\sqrt{5}}{\sqrt{10}}=\frac{\sqrt{2}}{2}$。

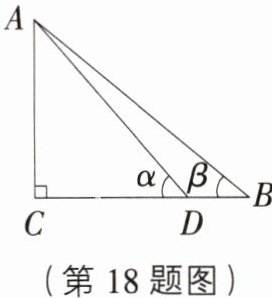
13. 重点[浙江丽水期末]如图,在Rt△ABC中,∠C = 90°,AC = 2,AB = 3.
(1)求BC的长;
(2)求sinA的值.
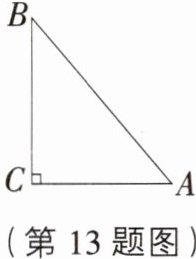
(1)求BC的长;
(2)求sinA的值.


答案:
[解析]
(1)在Rt△ABC中,∠C = 90°,AC = 2,AB = 3,
∴$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{3^{2}-2^{2}}=\sqrt{5}$;
(2)在Rt△ABC中,∠C = 90°,AB = 3,$BC=\sqrt{5}$,
∴$\sin A=\frac{BC}{AB}=\frac{\sqrt{5}}{3}$。
(1)在Rt△ABC中,∠C = 90°,AC = 2,AB = 3,
∴$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{3^{2}-2^{2}}=\sqrt{5}$;
(2)在Rt△ABC中,∠C = 90°,AB = 3,$BC=\sqrt{5}$,
∴$\sin A=\frac{BC}{AB}=\frac{\sqrt{5}}{3}$。
14. [广西河池中考]在Rt△ABC中,∠C = 90°,BC = 5,AC = 12,则sinB的值是 ( )
A. $\frac{5}{12}$
B. $\frac{12}{5}$
C. $\frac{5}{13}$
D. $\frac{12}{13}$
A. $\frac{5}{12}$
B. $\frac{12}{5}$
C. $\frac{5}{13}$
D. $\frac{12}{13}$
答案:
D [解析]如图,
∵∠C = 90°,BC = 5,AC = 12,
∴$AB=\sqrt{5^{2}+12^{2}} = 13$,
∴$\sin B=\frac{AC}{AB}=\frac{12}{13}$。

D [解析]如图,
∵∠C = 90°,BC = 5,AC = 12,
∴$AB=\sqrt{5^{2}+12^{2}} = 13$,
∴$\sin B=\frac{AC}{AB}=\frac{12}{13}$。

15. [云南中考]在△ABC中,∠ABC = 90°.若AC = 100,sinA = $\frac{3}{5}$,则AB的长是 ( )
A. $\frac{500}{3}$
B. $\frac{503}{3}$
C. 60
D. 80
A. $\frac{500}{3}$
B. $\frac{503}{3}$
C. 60
D. 80
答案:
D [解析]已知$\sin A=\frac{BC}{AC}=\frac{3}{5}$,AC = 100,解得BC = 60,
∴$AB=\sqrt{AC^{2}-BC^{2}} = 80$。
∴$AB=\sqrt{AC^{2}-BC^{2}} = 80$。
16. [广西桂林中考]如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是 ( )

A. $\frac{3}{4}$
B. $\frac{4}{3}$
C. $\frac{3}{5}$
D. $\frac{4}{5}$

A. $\frac{3}{4}$
B. $\frac{4}{3}$
C. $\frac{3}{5}$
D. $\frac{4}{5}$
答案:
D [解析]过点P作PA⊥x轴于点A,如图.
∵P(3,4),
∴OA = 3,AP = 4,
∴$OP=\sqrt{3^{2}+4^{2}} = 5$,
∴$\sin\alpha=\frac{AP}{OP}=\frac{4}{5}$。

D [解析]过点P作PA⊥x轴于点A,如图.
∵P(3,4),
∴OA = 3,AP = 4,
∴$OP=\sqrt{3^{2}+4^{2}} = 5$,
∴$\sin\alpha=\frac{AP}{OP}=\frac{4}{5}$。

17. [浙江湖州中考]如图,已知在Rt△ABC中,∠ACB = 90°,AC = 1,AB = 2,则sinB的值是______.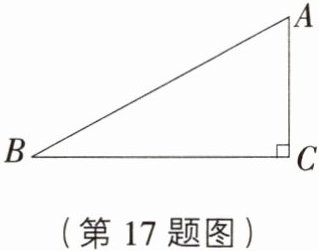

答案:
$\frac{1}{2}$ [解析]
∵∠ACB = 90°,AC = 1,AB = 2,
∴$\sin B=\frac{AC}{AB}=\frac{1}{2}$。
∵∠ACB = 90°,AC = 1,AB = 2,
∴$\sin B=\frac{AC}{AB}=\frac{1}{2}$。
18. [河北石家庄名校内测]如图,在Rt△ABC中,∠C = 90°,D为BC边(除端点外)上的一点,设∠ADC = α,∠B = β.
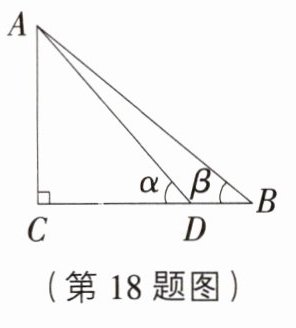
(1)猜想sinα与sinβ的大小关系;
(2)试证明你的结论.

(1)猜想sinα与sinβ的大小关系;
(2)试证明你的结论.
答案:
[解析]
(1)$\sin\alpha>\sin\beta$;
(2)证明:
∵$\sin\alpha=\frac{AC}{AD}$,$\sin\beta=\frac{AC}{AB}$,又
∵AD<AB,
∴$\sin\alpha>\sin\beta$。
(1)$\sin\alpha>\sin\beta$;
(2)证明:
∵$\sin\alpha=\frac{AC}{AD}$,$\sin\beta=\frac{AC}{AB}$,又
∵AD<AB,
∴$\sin\alpha>\sin\beta$。
查看更多完整答案,请扫码查看


