第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
1. 已知点(-3,2)在反比例函数$y=\frac{k}{x}$的图象上,则k的值为 ( )
A. -3
B. 3
C. -6
D. 6
A. -3
B. 3
C. -6
D. 6
答案:
C
2. (济宁中考)已知点A(-2,y1),B(-1,y2),C(3,y3)在反比例函数$y=\frac{k}{x}(k<0)$的图象上,则y1,y2,y3的大小关系是 ( )
A. y1<y2<y3
B. y2<y1<y3
C. y3<y1<y2
D. y3<y2<y1
A. y1<y2<y3
B. y2<y1<y3
C. y3<y1<y2
D. y3<y2<y1
答案:
C
3. 对于反比例函数$y=-\frac{6}{x}$,有下列结论:① 图象位于第二、第四象限;② 当x<0时,y随x的增大而增大;③ 从图象上任意一点作两坐标轴的垂线,与坐标轴围成的矩形面积都是6;④ 若点A(x1,y1),B(x2,y2)都在该函数图象上,且x1<x2,则y1<y2. 其中,正确的是 ( )
A. ①②③
B. ②③④
C. ①③④
D. ①②③④
A. ①②③
B. ②③④
C. ①③④
D. ①②③④
答案:
A
4. ★如图,P是反比例函数$y=\frac{k}{x}(x<0)$的图象上一点,过点P作PA⊥y轴于点A,B是点A关于x轴的对称点,连接PB. 若△PAB的面积为18,则k的值为 ( )
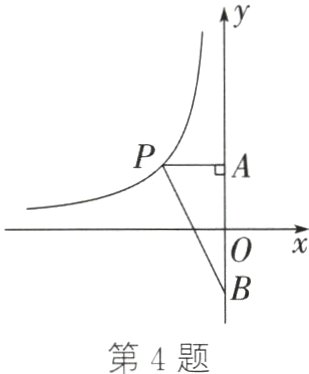
A. 18
B. 36
C. -18
D. -36

A. 18
B. 36
C. -18
D. -36
答案:
C
5. 在反比例函数$y=\frac{1 + 2m}{x}$的图象上有两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,则m的最小整数值为______.
答案:
0
6. ★(陕西中考)已知点A(-2,y1)和点B(m,y2)均在反比例函数$y=-\frac{5}{x}$的图象上. 若0<m<1,则y1 + y2______0(填“>”“<”或“=”).

答案:
< 解析:
∵点A(−2,y₁)和点B(m,y₂)均在反比例函数y=−$\frac{5}{x}$的图象上,
∴y₁=$\frac{5}{2}$,y₂ = - $\frac{5}{m}$。
∵0<m<1,
∴y₂<−5。
∴y₁+y₂<$\frac{5}{2}$−5=−$\frac{5}{2}$<0。
∵点A(−2,y₁)和点B(m,y₂)均在反比例函数y=−$\frac{5}{x}$的图象上,
∴y₁=$\frac{5}{2}$,y₂ = - $\frac{5}{m}$。
∵0<m<1,
∴y₂<−5。
∴y₁+y₂<$\frac{5}{2}$−5=−$\frac{5}{2}$<0。
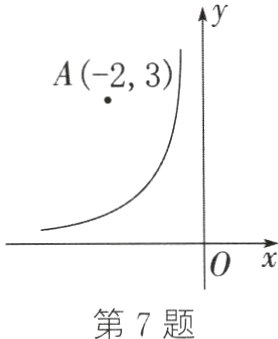
7. ★如图所示为反比例函数$y=\frac{k}{x}$的图象,则k的取值范围是______.
答案:
−6<k<0 解析:由题图可知,k<0。
∵点A(−2,3)在函数图象的上方,
∴当x=−2时,y=$\frac{k}{−2}$<3。
∴k>−6,即−6<k<0。
∵点A(−2,3)在函数图象的上方,
∴当x=−2时,y=$\frac{k}{−2}$<3。
∴k>−6,即−6<k<0。
8. (15分)(广安中考)如图,一次函数y = ax + b(a,b为常数)的图象与反比例函数$y=\frac{k}{x}$(k为常数)的图象交于A(2,4),B(n,-2)两点.
(1)求一次函数和反比例函数的解析式;
(2)直线AB与x轴交于点C,P(m,0)是x轴上的点,若△PAC的面积大于12,请直接写出m的取值范围.
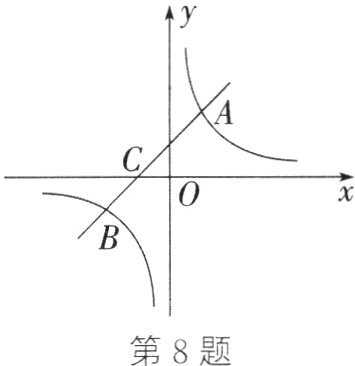
(1)求一次函数和反比例函数的解析式;
(2)直线AB与x轴交于点C,P(m,0)是x轴上的点,若△PAC的面积大于12,请直接写出m的取值范围.

答案:
(1)把A(2,4)代入y=$\frac{k}{x}$,得k=8,
∴反比例函数的解析式为y=$\frac{8}{x}$。把B(n,−2)代入y=$\frac{8}{x}$,得n=−4,
∴B(−4,−2)。
∵点A(2,4),B(−4,−2)都在一次函数y=ax + b的图象上,
∴$\begin{cases}2a + b = 4 \\ -4a + b = -2 \end{cases}$,解得$\begin{cases}a = 1 \\ b = 2 \end{cases}$,
∴一次函数的解析式为y = x + 2。
(2)m>4或m<−8 解析:在y = x + 2中,令y = 0,则x = -2,
∴C(−2,0)。
∵点P的坐标为(m,0),
∴PC = |m + 2|。
∵$S_{\triangle PAC}$ = $\frac{1}{2}$×|m + 2|×4>12,
∴|m + 2|>6,解得m>4或m<−8。
(1)把A(2,4)代入y=$\frac{k}{x}$,得k=8,
∴反比例函数的解析式为y=$\frac{8}{x}$。把B(n,−2)代入y=$\frac{8}{x}$,得n=−4,
∴B(−4,−2)。
∵点A(2,4),B(−4,−2)都在一次函数y=ax + b的图象上,
∴$\begin{cases}2a + b = 4 \\ -4a + b = -2 \end{cases}$,解得$\begin{cases}a = 1 \\ b = 2 \end{cases}$,
∴一次函数的解析式为y = x + 2。
(2)m>4或m<−8 解析:在y = x + 2中,令y = 0,则x = -2,
∴C(−2,0)。
∵点P的坐标为(m,0),
∴PC = |m + 2|。
∵$S_{\triangle PAC}$ = $\frac{1}{2}$×|m + 2|×4>12,
∴|m + 2|>6,解得m>4或m<−8。
查看更多完整答案,请扫码查看


