《2025年通城学典活页检测九年级数学下册人教版》

11. (12分)求下列各式中锐角α的度数:
　　(1) sin(α - 20°) = $\frac{\sqrt{3}}{2}$;　　　　(2) 2cos(α + 30°) = 1;　　　　(3) 3tan(2α + 10°) = $\sqrt{3}$.

答案：
(1)由题意,得α−20°=60°,解得α=80°　
(2)由题意，得cos(α+30°)=$\frac{1}{2}$，
∴α+30°=60°,解得α=30°　
(3)由题意，得tan(2α+10°)=$\frac{\sqrt{3}}{3}$，
∴2α+10°=30°,解得α=10°

12. ★(12分)阅读材料并解决问题:
　　　初中阶段，我们所学的锐角三角函数反映了直角三角形中的边角关系. 一般地，当α,β为任意角时,sin(α + β)与sin(α - β)的值可以用下面的公式求得:sin(α + β) = sinαcosβ + cosαsinβ,sin(α - β) = sinαcosβ - cosαsinβ. 例如:sin15° = sin(45° - 30°) = sin45°cos30° - cos45°sin30° = $\frac{\sqrt{2}}{2}$×$\frac{\sqrt{3}}{2}$ - $\frac{\sqrt{2}}{2}$×$\frac{1}{2}$ = $\frac{\sqrt{6}-\sqrt{2}}{4}$.
　　(1) 计算:sin75° = ________;
　　(2) 在Rt△ABC中,∠A = 75°,∠C = 90°,AB = 4,求AC和BC的长.

答案：
(1)$\frac{\sqrt{2}+\sqrt{6}}{4}$　
(2)在Rt△ABC中，
∵sinA=sin75°=$\frac{BC}{AB}$=$\frac{\sqrt{2}+\sqrt{6}}{4}$，
∴BC=AB×$\frac{\sqrt{2}+\sqrt{6}}{4}$=4×$\frac{\sqrt{2}+\sqrt{6}}{4}$=$\sqrt{2}$+$\sqrt{6}$。
∵∠B=90°−∠A，
∴∠B=15°。
∵sinB=sin15°=$\frac{AC}{AB}$=$\frac{\sqrt{6}-\sqrt{2}}{4}$，
∴AC=AB×$\frac{\sqrt{6}-\sqrt{2}}{4}$=4×$\frac{\sqrt{6}-\sqrt{2}}{4}$=$\sqrt{6}-\sqrt{2}$

13. ★(14分)
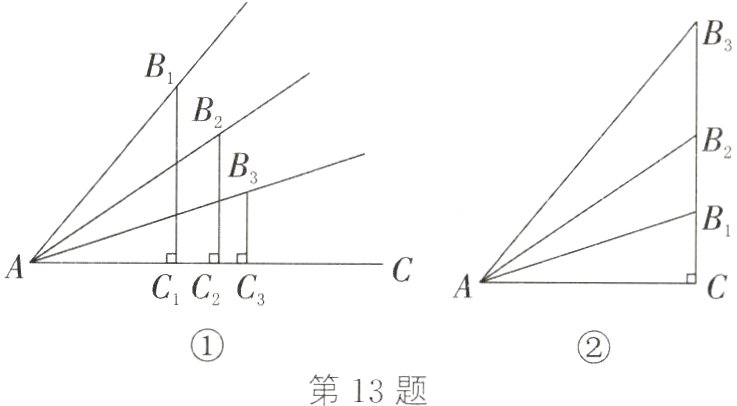
　　(1) 如图,锐角的正弦值和余弦值都随着锐角度数的变化而变化,试探索随着锐角度数的增大，它的正弦值和余弦值变化的规律.
　　(2) 根据(1)中探索到的规律，比较18°,34°,52°,65°,88°的正弦值的大小和余弦值的大小.
　　(3) 若α = 45°,则sinα ________cosα;若0°＜α＜45°,则sinα ________cosα;若45°＜α＜90°则sinα ________cosα(填“＞”“＜"或“=”).
　　(4) 利用互为余角的两个角的正弦值和余弦值的大小关系，比较sin10°,cos30°,sin50°,cos70°的大小.
　

答案：
(1)在题图①中，令$AB_{1}=AB_{2}=AB_{3}$，$B_{1}C_{1}\perp AC$于点$C_{1}$，$B_{2}C_{2}\perp AC$于点$C_{2}$，$B_{3}C_{3}\perp AC$于点$C_{3}$，显然有$B_{1}C_{1}＞B_{2}C_{2}＞B_{3}C_{3}$，$\angle B_{1}AC＞\angle B_{2}AC＞\angle B_{3}AC$。又
∵sin∠$B_{1}AC=\frac{B_{1}C_{1}}{AB_{1}}$，sin∠$B_{2}AC=\frac{B_{2}C_{2}}{AB_{2}}$，sin∠$B_{3}AC=\frac{B_{3}C_{3}}{AB_{3}}$，
∴sin∠$B_{1}AC＞$sin∠$B_{2}AC＞$sin∠$B_{3}AC$，即锐角的正弦值随着锐角度数的增大而增大。在题图②中，∠C = 90°，cos∠$B_{1}AC=\frac{AC}{AB_{1}}$，cos∠$B_{2}AC=\frac{AC}{AB_{2}}$，cos∠$B_{3}AC=\frac{AC}{AB_{3}}$，且∠$B_{1}AC＜$∠$B_{2}AC＜$∠$B_{3}AC$。
∵$AB_{1}＜AB_{2}＜AB_{3}$，
∴$\frac{AC}{AB_{1}}＞\frac{AC}{AB_{2}}＞\frac{AC}{AB_{3}}$，
∴cos∠$B_{1}AC＞$cos∠$B_{2}AC＞$cos∠$B_{3}AC$，即锐角的余弦值随着锐角度数的增大而减小。
(2)sin18°＜sin34°＜sin52°＜sin65°＜sin88°，cos18°＞cos34°＞cos52°＞cos65°＞cos88°　
(3)=　＜　＞　
(4)
∵易得cos30°=sin60°，cos70°=sin20°，sin60°＞sin50°＞sin20°＞sin10°，
∴cos30°＞sin50°＞cos70°＞sin10°