《2025年通城学典活页检测九年级数学下册人教版》

7. ★(22分)(宜宾中考)某同学在数学实践中测量长江口的宽度，他在长江口的两岸选择两点C，D，在地标广场上选择两个观测点A，B(点A，B，C，D在同一水平面上，且AB//CD). 如图，在点A处测得点C在北偏西18.17°方向上，测得点D在北偏东21.34°方向上；在点B处测得点C在北偏西21.34°方向上，测得点D在北偏东18.17°方向上，测得AB＝100 m. 求长江口的宽度CD(结果取整数，参考数据：$\sin 18.17^{\circ}\approx0.31$，$\cos 18.17^{\circ}\approx0.95$，$\tan 18.17^{\circ}\approx0.33$，$\sin 21.34^{\circ}\approx0.36$，$\cos 21.34^{\circ}\approx0.93$，$\tan 21.34^{\circ}\approx0.39$).
　　

答案：
如图，过点A作AE⊥CD,垂足为E,过点B作BF⊥CD,垂足为F.
∵AB//CD,
∴AE=BF.由题意，易得AB=EF=100m.设AE=BF=xm.在Rt△ACE中,∠CAE=18.17°,
∴CE=AE·tan∠CAE≈0.33xm.在Rt△BDF中,∠DBF=18.17°,
∴DF=BF·tan∠DBF≈0.33xm.在Rt△AED中,∠EAD=21.34°,
∴DE=AE·tan∠EAD≈0.39xm.
∵DE=EF+DF,
∴0.39x=100+0.33x,解得x=$\frac{5000}{3}$.
∴CD=CE+DE=0.33×$\frac{5000}{3}$+0.39×$\frac{5000}{3}$=1200(m).
∴长江口的宽度CD约为1200m
　　　　　　　　　

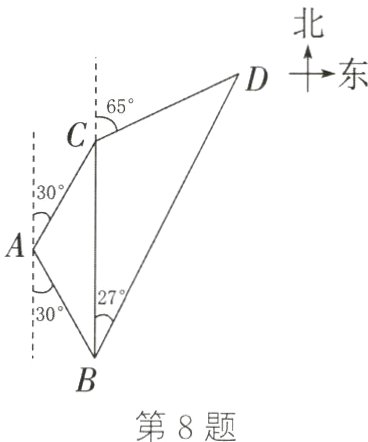
8. ★(24分)(资阳中考)如图，某海域有两灯塔A，B，其中灯塔B在灯塔A的南偏东30°方向上，且A，B相距$\frac{16\sqrt{3}}{3}$海里. 一渔船在C处捕鱼，测得C处在灯塔A的北偏东30°方向上、灯塔B的正北方向上.
　(1) 求B，C两处的距离.
　(2) 该渔船从C处沿北偏东65°方向航行一段时间后，突发故障滞留于D处，并发出求救信号. 此时，在灯塔B处的渔政船测得D处在北偏东27°方向上，便立即以18海里/时的速度沿BD方向航行至D处救援，求渔政船的航行时间(点A，B，C，D在同一水平面上，参考数据：$\tan 65^{\circ}\approx2.1$，$\tan 27^{\circ}\approx0.5$).
　　　　

答案：

(1)由题意,得∠ACB=∠ABC=30°,
∴AB=AC=$\frac{16\sqrt{3}}{3}$海里.如图，过点A作AH⊥BC于点H,则∠AHC=∠AHB=90°,CH=BH.
∴CH=BH=AB·cos30°=$\frac{16\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$=8(海里).
∴BC=8+8=16(海里),即B，C两处的距离为16海里　
(2)如图，过点D作DG⊥BC于点G.在Rt△BDG中,BG=$\frac{DG}{tan27°}$≈$\frac{DG}{0.5}$=2DG,在Rt△CDG中,CG=$\frac{DG}{tan65°}$≈$\frac{DG}{2.1}$.
∵BC=BG−CG,
∴2DG−$\frac{DG}{2.1}$=16.
∴DG=10.5海里.
∴CG=5海里.
∴BG=BC+CG=21海里.
∴在Rt△BDG中，由勾股定理，得BD=$\sqrt{BG²+DG²}$=$\frac{21\sqrt{5}}{2}$海里.
∴渔政船的航行时间约为$\frac{21\sqrt{5}}{2}$÷18=$\frac{7\sqrt{5}}{12}$(时)