《2025年通城学典活页检测九年级数学下册人教版》

8. (14分)(常州中考)如图，一幅书画在装裱前的大小是1.2 m×0.8 m. 装裱后，上、下、左、右边衬的宽度分别是a m，b m，c m，d m. 若装裱后AB与AD的比是16 : 10，且a = b，c = d，c = 2a，求四周边衬的宽度.
　

答案： 由题意，得$AB=(1.2 + c + d)\text{m}$，$AD=(0.8 + a + b)\text{m}$，
$\because a = b$，$c = d$，$c = 2a$，$\therefore AB=(1.2 + c + d)\text{m}=(1.2 + 4a)\text{m}$，
$AD=(0.8 + a + b)\text{m}=(0.8 + 2a)\text{m}$.$\because AB$与$AD$的比是$16:10$，
$\therefore (1.2 + 4a):(0.8 + 2a)=16:10$.$\therefore a = 0.1$.$\therefore b = 0.1$，$c = d = 0.2$.$\therefore$上、下、左、右边衬的宽度分别是$0.1\text{ m}$，$0.1\text{ m}$，$0.2\text{ m}$，$0.2\text{ m}$

9. (18分)如图，在直角坐标系中，△ABC的三个顶点坐标分别为A(-2，3)，B(-3，1)，C(-1，2).
(1) 将△ABC绕点O顺时针旋转90°得到△A₁B₁C₁，画出△A₁B₁C₁，并写出点B₁的坐标.
(2) 将△ABC的三个顶点坐标分别乘-2，得到对应的点A₂，B₂，C₂，画出△A₂B₂C₂，并判断△ABC与△A₂B₂C₂是否是位似图形. 若是，直接写出△ABC与△A₂B₂C₂的位似中心的坐标及相似比.
　　　　

答案：
（1）如图，$\triangle A_{1}B_{1}C_{1}$即为所求 点$B_{1}$的坐标为$(1,3)$ （2）由题意，得$A_{2}(4,-6)$，$B_{2}(6,-2)$，$C_{2}(2,-4)$ 如图，$\triangle A_{2}B_{2}C_{2}$即为所求 是 位似中心的坐标为$(0,0)$，相似比为$\frac{1}{2}$

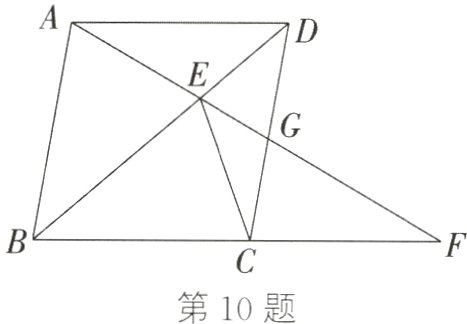
10. ★(20分)如图，在菱形ABCD中，点G在边CD上，连接AG并延长交BC的延长线于点F，连接BD交AF于点E，连接CE.
(1) 若BE = BC，∠ABC = 80°，求∠DAE的度数；
(2) 求证：$EC^{2}=EF\cdot EG$；
(3) 若AB = 6，$\frac{CE}{EG}=3$，求CF的长.
　　　　

答案： （1）$\because$四边形$ABCD$是菱形，$\therefore AB = BC$，$AD// BC$，$\angle ABD=\frac{1}{2}\angle ABC = 40^{\circ}$.$\therefore \angle BAD = 180^{\circ}-\angle ABC = 180^{\circ}-80^{\circ}=100^{\circ}$.
$\because BE = BC$，$\therefore AB = BE$.$\therefore \angle BAE=\frac{180^{\circ}-\angle ABE}{2}=\frac{180^{\circ}-40^{\circ}}{2}=70^{\circ}$.$\therefore \angle DAE=\angle BAD-\angle BAE = 100^{\circ}-70^{\circ}=30^{\circ}$
（2）$\because$四边形$ABCD$是菱形，$\therefore DA = DC$，$\angle ADE=\angle CDE$.又$\because DE = DE$，$\therefore \triangle ADE\cong\triangle CDE$.$\therefore \angle DAE=\angle DCE$.$\because AD// BC$，$\therefore \angle DAE=\angle F$.$\therefore \angle DCE=\angle F$.又$\because \angle CEF=\angle GEC$，
$\therefore \triangle CEG\backsim\triangle FEC$.$\therefore \frac{GE}{CE}=\frac{EC}{EF}$，即$EC^{2}=EF\cdot EG$ （3）$\because$四边形$ABCD$是菱形，$\therefore AD = AB = 6$.由（2），知$\triangle ADE\cong\triangle CDE$，
$\therefore AE = CE$.设$EG = a$，则$AE = CE = 3a$.$\because EC^{2}=EF\cdot EG$，
$\therefore EF = 9a$.$\therefore AG = AE + EG = 3a + a = 4a$，$FG = EF - EG = 9a - a = 8a$.$\because AD// BC$，$\therefore \angle ADG=\angle DCF$，$\angle DAF=\angle F$.
$\therefore \triangle ADG\backsim\triangle FCG$.$\therefore \frac{CF}{AD}=\frac{FG}{AG}=\frac{8a}{4a}=2$.$\therefore CF = 2AD = 2\times6 = 12$