第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
6. ★(盐城中考)如图,小明用无人机测量教学楼的高度,将无人机垂直上升至距地面30 m的点P处,测得教学楼底端点A的俯角为37°,再将无人机沿教学楼方向水平飞行26.6 m至点Q处,测得教学楼顶端点B的俯角为45°,则教学楼AB的高度约为________m(结果取整数,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75).


答案:
17
7. (22分)(青海中考)如图,某种摄像头识别到最远点A的俯角α是17°,识别到最近点B的俯角β是45°,该摄像头安装在距地面5 m的点C处,求最远点与最近点之间的距离AB(结果取整数,参考数据:sin 17°≈0.29,cos 17°≈0.96,tan 17°≈0.31).


答案:
如图,由题意,得CE//AD,CD=5m,
∴∠A=∠α=17°,∠CBD=∠β=45°.在Rt△ACD中,
∵CD=5m,
∴tanA=tan17°=CD/AD≈0.31.
∴AD=5/0.31≈16.1(m).在Rt△BCD中,
∵∠CBD=45°,
∴∠BCD=90°−45°=45°.
∴∠BCD=∠CBD.
∴BD=CD=5m.
∴AB=AD−BD=16.1−5≈11(m).
∴最远点与最近点之间的距离AB约是11m

如图,由题意,得CE//AD,CD=5m,
∴∠A=∠α=17°,∠CBD=∠β=45°.在Rt△ACD中,
∵CD=5m,
∴tanA=tan17°=CD/AD≈0.31.
∴AD=5/0.31≈16.1(m).在Rt△BCD中,
∵∠CBD=45°,
∴∠BCD=90°−45°=45°.
∴∠BCD=∠CBD.
∴BD=CD=5m.
∴AB=AD−BD=16.1−5≈11(m).
∴最远点与最近点之间的距离AB约是11m

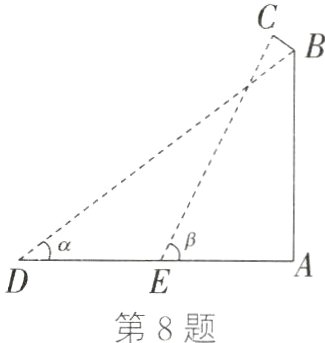
8. ★(24分)如图所示为一种户外景观灯的示意图,它是由灯杆AB和灯管支架BC两部分构成. 现测得灯管支架BC与灯杆AB的夹角∠ABC=127°,同学们想知道灯管支架BC的长度,借助相关仪器进行测量后结果如下表:
|测量项目|测量数据|
|--|--|
|从D处测得灯杆顶部B处仰角α|α=37°|
|从E处测得灯管支架C处仰角β|β=63°26′|
|两次测量之间的水平距离|DE=5.1 m|
|灯杆的高度|AB=8.1 m|
求灯管支架BC的长度(参考数据:sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75,tan 63°26′≈2).
|测量项目|测量数据|
|--|--|
|从D处测得灯杆顶部B处仰角α|α=37°|
|从E处测得灯管支架C处仰角β|β=63°26′|
|两次测量之间的水平距离|DE=5.1 m|
|灯杆的高度|AB=8.1 m|
求灯管支架BC的长度(参考数据:sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75,tan 63°26′≈2).

答案:
如图,延长AB,EC交于点F.由题意,得∠A=90°.在Rt△ADB 中,tanα=AB/AD,
∴tan37°=8.1/AD≈0.75.
∴AD=10.8m.
∵DE=5.1m,
∴AE=AD−DE=5.7m.在Rt△AEF中,tanβ=AF/AE,
∴tan63°26′=AF/5.7≈2.
∴AF=11.4m.
∴BF=AF−AB=3.3m.过点C作CH⊥AF于点H,则∠CHF=∠CHB=90°.
∴∠CHF=∠A.
∴CH//AE.
∴∠FCH=∠FEA=63°26'.
∵∠ABC=127°,
∴∠CBH=53°.
∴∠BCH=37°.
∴FH=CH·tan∠FCH,BH=CH·tan∠BCH.
∴BF=FH+BH=CH·tan∠FCH+CH·tan∠BCH=CH·(2 + 0.75)=2.75CH.
∵BF=3.3m,
∴CH=1.2m.
∴BC=CH/cos∠BCH≈1.2/0.8 = 1.5(m),即灯管支架BC的长度约为1.5m

如图,延长AB,EC交于点F.由题意,得∠A=90°.在Rt△ADB 中,tanα=AB/AD,
∴tan37°=8.1/AD≈0.75.
∴AD=10.8m.
∵DE=5.1m,
∴AE=AD−DE=5.7m.在Rt△AEF中,tanβ=AF/AE,
∴tan63°26′=AF/5.7≈2.
∴AF=11.4m.
∴BF=AF−AB=3.3m.过点C作CH⊥AF于点H,则∠CHF=∠CHB=90°.
∴∠CHF=∠A.
∴CH//AE.
∴∠FCH=∠FEA=63°26'.
∵∠ABC=127°,
∴∠CBH=53°.
∴∠BCH=37°.
∴FH=CH·tan∠FCH,BH=CH·tan∠BCH.
∴BF=FH+BH=CH·tan∠FCH+CH·tan∠BCH=CH·(2 + 0.75)=2.75CH.
∵BF=3.3m,
∴CH=1.2m.
∴BC=CH/cos∠BCH≈1.2/0.8 = 1.5(m),即灯管支架BC的长度约为1.5m

查看更多完整答案,请扫码查看


