《2025年通城学典活页检测九年级数学下册人教版》

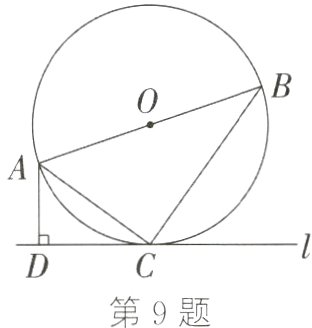
9.(14分)(盐城中考)如图，点C在以AB为直径的⊙O上，过点C作⊙O的切线l，过点A作AD⊥l，垂足为D，连接AC，BC.
(1)求证：△ABC∽△ACD；
(2)若AC = 5，CD = 4，求⊙O的半径.
　　　　

答案：
（1）如图，连接OC.
∵ OC是⊙O的半径，l是⊙O的切线，
∴ OC⊥l.
∵ AD⊥l，
∴ OC//AD.
∴ ∠CAD = ∠ACO.
∵ OA = OC，
∴ ∠ACO = ∠BAC.
∴ ∠CAD = ∠BAC.
∵ AB为⊙O的直径，AD⊥l，
∴ ∠ADC = ∠ACB = 90°.
∴ △ABC∽△ACD （2）在Rt△ADC中，AC = 5，CD = 4，由勾股定理，得AD = $\sqrt{AC^{2}-CD^{2}}$ = 3.
∵ △ABC∽△ACD，
∴ $\frac{AB}{AC}$ = $\frac{AC}{AD}$.
∴ $\frac{AB}{5}$ = $\frac{5}{3}$.
∴ AB = $\frac{25}{3}$.
∴ ⊙O的半径为$\frac{25}{6}$

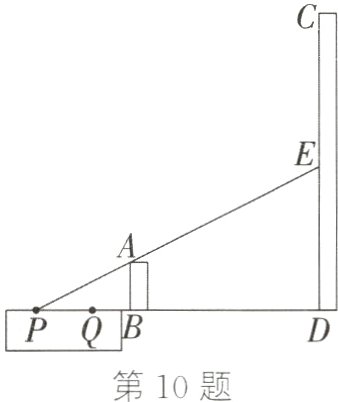
10.(18分)如图，在某次军事演习中，涂色部分为我军地面以下的战壕，前方有两栋楼房AB，CD，已知AB = 10米，CD = 62米，敌军在楼房CD中与我军对抗，我军一名战士在距离点B 20米的点P处观测，视线PA经过点A落到CD上的点E处，ED = 30米，点P，B，D在一条直线上.该战士向点B的方向行走12米到点Q处观测，他此时能否看到楼房CD的最高点C？请通过计算说明理由.
　　　　　　　　　

答案：
他此时能看到楼房CD的最高点C 理由：由题意，得AB//CD，
∴ △APB∽△EPD.
∴ $\frac{AB}{ED}$ = $\frac{PB}{PD}$，即$\frac{10}{30}$ = $\frac{20}{PD}$.
∴ PD = 60米.
∴ BD = PD - PB = 60 - 20 = 40（米）. 如图，连接QA并延长，交直线CD于点F.
∵ AB//CD，
∴ △ABQ∽△FDQ.
∴ $\frac{AB}{FD}$ = $\frac{QB}{QD}$.
∵ QB = PB - PQ = 20 - 12 = 8（米），QD = PD - PQ = 60 - 12 = 48（米），
∴ $\frac{10}{FD}$ = $\frac{8}{48}$.
∴ FD = 60米.
∵ 60＜62，
∴ 他此时能看到楼房CD的最高点C.

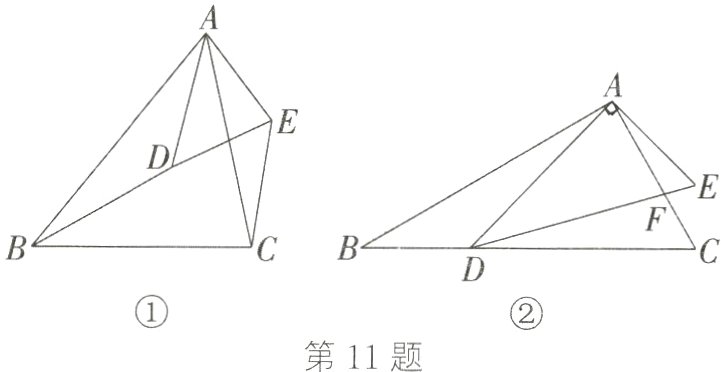
11. ★(20分)
(1)如图①，△ABC∽△ADE，连接BD，CE，求证：△ABD∽△ACE；
(2)如图②，在△ABC和△ADE中，∠BAC = ∠DAE = 90°，∠ABC = ∠ADE = 30°，点D在边BC上，AC与DE相交于点F，且$\frac{AD}{BD}=\sqrt{3}$，求$\frac{AF}{EF}$的值.
　　　　　　　　　　　　　　　　　　　　　　　

答案：
（1）
∵ △ABC∽△ADE，
∴ $\frac{AB}{AD}$ = $\frac{AC}{AE}$，∠BAC = ∠DAE.
∴ $\frac{AB}{AC}$ = $\frac{AD}{AE}$，∠BAC - ∠DAC = ∠DAE - ∠DAC.
∴ ∠BAD = ∠CAE.
∴ △ABD∽△ACE （2）如图，连接EC.
∵ ∠BAC = ∠DAE = 90°，∠ABC = ∠ADE = 30°，
∴ △ABC∽△ADE. 由（1），得△ABD∽△ACE，
∴ $\frac{BD}{CE}$ = $\frac{AD}{AE}$，∠ACE = ∠ABD = ∠ADE.
∴ $\frac{AE}{CE}$ = $\frac{AD}{BD}$ = $\sqrt{3}$. 在Rt△ADE中，
∵ ∠ADE = 30°，
∴ DE = 2AE.
∴ 由勾股定理，得AD = $\sqrt{DE^{2}-AE^{2}}$ = $\sqrt{3}$AE.
∴ $\frac{AD}{AE}$ = $\sqrt{3}$.
∴ $\frac{AD}{EC}$ = $\frac{AD}{AE}$·$\frac{AE}{EC}$ = $\sqrt{3}$×$\sqrt{3}$ = 3.
∵ ∠ADF = ∠ECF，∠AFD = ∠EFC，
∴ △ADF∽△ECF.
∴ $\frac{AF}{EF}$ = $\frac{AD}{EC}$ = 3