《2025年通城学典活页检测九年级数学下册人教版》

10. (12分)在Rt△ABC中，∠C = 90°，a，b，c分别为∠A，∠B，∠C的对边，分别根据下列条件解直角三角形.
(1)∠B = 60°，a = 4； (2)a = $\sqrt{3}-1$，b = 3 - $\sqrt{3}$； (3)∠A = 60°，c = 2 + $\sqrt{3}$.

答案：
(1)
∵∠B=60°,∠C=90°,
∴∠A=30°.
∵tanB=$\frac{b}{a}$,
∴b=atanB=4×tan60°=$4\sqrt{3}$.
∵cosB=$\frac{a}{c}$，
∴c=$\frac{a}{cosB}$ = $\frac{4}{cos60°}$ = 8.
(2)
∵∠C=90°,
∴tanB=$\frac{b}{a}$=$\frac{3−\sqrt{3}}{\sqrt{3}−1}$=$\sqrt{3}$.
∴∠B=60°.
∴∠A=30°.
∵sinA=$\frac{a}{c}$,
∴c=$\frac{a}{sinA}$=$\frac{\sqrt{3}−1}{sin30°}$ = $2\sqrt{3}-2$.
(3)
∵∠A=60°,∠C=90°,
∴∠B=30°.
∵sinA=$\frac{a}{c}$,
∴a=csinA=(2+$\sqrt{3}$)×sin60°=$\sqrt{3}+\frac{3}{2}$.
∵cosA=$\frac{b}{c}$,
∴b=ccosA=(2+$\sqrt{3}$)×cos60°=$1+\frac{\sqrt{3}}{2}$.

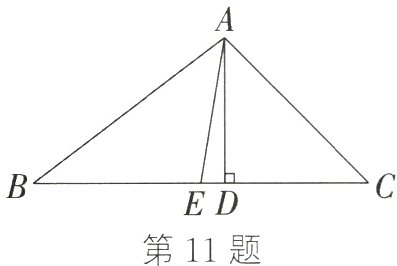
11. (14分)(浙江中考)如图，在△ABC中，AD⊥BC于点D，AE是边BC上的中线，AB = 10，AD = 6，tan∠ACB = 1. 求：
(1)BC的长；
(2)sin∠DAE的值.
　　　　

答案：
(1)
∵AD⊥BC,AB=10,AD=6,
∴在Rt△ABD中，由勾股定理,得BD = $\sqrt{AB^{2}-AD^{2}}$ = $\sqrt{10^{2}-6^{2}}$ = 8.
∵tan∠ACB = $\frac{AD}{CD}$ = 1,
∴CD=AD=6.
∴BC=BD+CD=8+6=14.
(2)
∵AE是边BC上的中线，
∴CE=$\frac{1}{2}$BC=7.
∴DE=CE−CD=7−6=1.
∵AD⊥BC,
∴在Rt△ADE中，由勾股定理，得AE = $\sqrt{AD^{2}+DE^{2}}$ = $\sqrt{6^{2}+1^{2}}$ = $\sqrt{37}$.
∴sin∠DAE=$\frac{DE}{AE}$ = $\frac{1}{\sqrt{37}}$ = $\frac{\sqrt{37}}{37}$.

12. ★(20分)(济宁中考)知识再现：如图①，在Rt△ABC中，∠C = 90°，∠A，∠B，∠C的对边分别为a，b，c. ∵sin A = $\frac{a}{c}$，sin B = $\frac{b}{c}$，∴c = $\frac{a}{sin A}$，c = $\frac{b}{sin B}$. ∴$\frac{a}{sin A}=\frac{b}{sin B}$.
(1)拓展探究：如图②，在锐角三角形ABC中，∠A，∠B，∠C的对边分别为a，b，c. 请探究$\frac{a}{sin A}$，$\frac{b}{sin B}$，$\frac{c}{sin C}$之间的关系，并写出探究过程.
(2)解决问题：如图③，为测量点A到河对岸点B的距离，选取与点A在河岸同一侧的点C，测得AC = 60 m，∠A = 75°，∠C = 60°. 请用拓展探究中的结论，求点A，B之间的距离.

答案：

(1)如图，过点C作CD⊥AB于点D,过点A作AE⊥BC于点E.在Rt△ABE中,sinB=$\frac{AE}{AB}$=$\frac{AE}{c}$;在Rt△BCD中,sinB=$\frac{CD}{BC}$=$\frac{CD}{a}$;在Rt△ACD中,sin∠BAC=$\frac{CD}{AC}$ = $\frac{CD}{b}$;在Rt△ACE 中,sin∠BCA=$\frac{AE}{AC}$=$\frac{AE}{b}$.
∴AE=csinB,CD=asinB,CD=bsin∠BAC,AE=bsin∠BCA.
∴csinB=bsin∠BCA,asinB=bsin∠BAC.
∴$\frac{b}{sinB}$ = $\frac{c}{sin∠BCA}$, $\frac{a}{sin∠BAC}$ = $\frac{b}{sinB}$.
∴$\frac{a}{sin∠BAC}$=$\frac{b}{sinB}$=$\frac{c}{sin∠BCA}$.
(2)在△ABC中,∠B=180°−∠A−∠C=180°−75°−60°=45°.
∵$\frac{AB}{sinC}$=$\frac{AC}{sinB}$,
∴$\frac{AB}{sin60°}$ = $\frac{60}{sin45°}$.
∴AB=$30\sqrt{6}$m,即点A,B之间的距离为$30\sqrt{6}$m.