第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
9. (14分)如图所示为反比例函数$y=\frac{4 - 2m}{x}$的图象的一支.
(1) 该函数图象的另一支在第______象限;
(2) $m$的取值范围是______;
(3) 若点$A(-2,y_1),B(-1,y_2),C(1,y_3)$都在这个反比例函数的图象上,试比较$y_1,y_2,y_3$的大小.
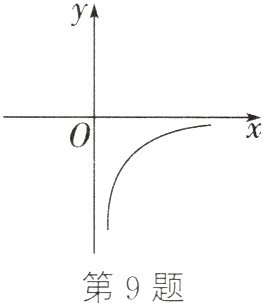
(1) 该函数图象的另一支在第______象限;
(2) $m$的取值范围是______;
(3) 若点$A(-2,y_1),B(-1,y_2),C(1,y_3)$都在这个反比例函数的图象上,试比较$y_1,y_2,y_3$的大小.

答案:
(1)二 (2)$m>2$ (3)由题意,得点A,B在第二象限的函数图象上,点C在第四象限的函数图象上,
∴ $y_1>0,y_2>0,y_3<0$.
∵在该反比例函数图象的每一支上,y随x的增大而增大,且$-2<-1<0$,
∴ $y_1<y_2$.
∴ $y_3<y_1<y_2$
∴ $y_1>0,y_2>0,y_3<0$.
∵在该反比例函数图象的每一支上,y随x的增大而增大,且$-2<-1<0$,
∴ $y_1<y_2$.
∴ $y_3<y_1<y_2$
10. (16分)(温州中考)反比例函数$y=\frac{k}{x}$的图象的一支如图所示,它经过点$(3,-2)$.
(1) 写出这个反比例函数的解析式,并补画该函数图象的另一支;
(2) 当$y\leq5$,且$y\neq0$时,求自变量$x$的取值范围.
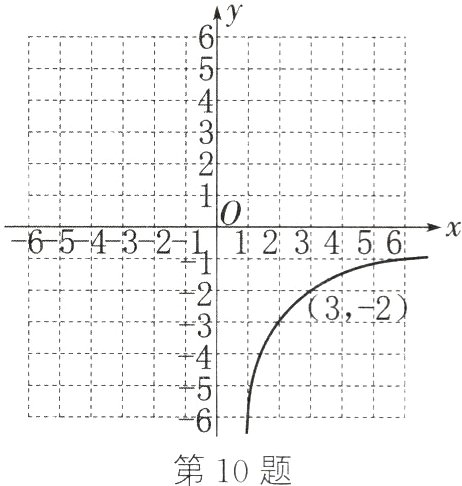
(1) 写出这个反比例函数的解析式,并补画该函数图象的另一支;
(2) 当$y\leq5$,且$y\neq0$时,求自变量$x$的取值范围.

答案:
(1)把(3, -2)代入$y=\frac{k}{x}$,得$-2=\frac{k}{3}$,解得$k=-6$.
∴反比例函数的解析式为$y=-\frac{6}{x}$ 补画该函数图象的另一支如图所示(2)当$y=5$时,$-\frac{6}{x}=5$,解得$x=-\frac{6}{5}$.
∴当$y\leq5$且$y≠0$时,$x\leq-\frac{6}{5}$或$x>0$
(1)把(3, -2)代入$y=\frac{k}{x}$,得$-2=\frac{k}{3}$,解得$k=-6$.
∴反比例函数的解析式为$y=-\frac{6}{x}$ 补画该函数图象的另一支如图所示(2)当$y=5$时,$-\frac{6}{x}=5$,解得$x=-\frac{6}{5}$.
∴当$y\leq5$且$y≠0$时,$x\leq-\frac{6}{5}$或$x>0$

11. ★★(18分)参照学习函数$y=\frac{2}{x}$的过程与方法,探究函数$y=\frac{2}{x - 2}(x\neq2)$的图象与性质.
|$x$|…|-2|-1|0|$\frac{1}{2}$|1|$\frac{3}{2}$|2|$\frac{5}{2}$|3|$\frac{7}{2}$|4|5|6|…|
|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|
|$y=\frac{2}{x}$|…|-1|-2|■|4|2|$\frac{4}{3}$|1|$\frac{4}{5}$|$\frac{2}{3}$|$\frac{4}{7}$|$\frac{1}{2}$|$\frac{2}{5}$|$\frac{1}{3}$|…|
|$y=\frac{2}{x - 2}$|…|$-\frac{1}{2}$|$-\frac{2}{3}$|-1|$m$|-2|-4|■|4|2|$\frac{4}{3}$|1|$\frac{2}{3}$|$\frac{1}{2}$|…|
(1) $m=$______.
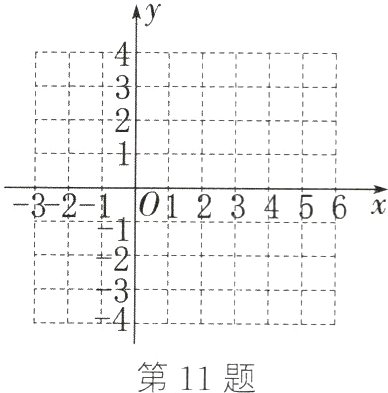
(2) 请画出函数$y=\frac{2}{x - 2}(x\neq2)$的图象.
(3) 观察图象并分析表格,回答下列问题:
① 当$x<2$时,$y$随$x$的增大而______(填“增大”或“减小”);
② 函数$y=\frac{2}{x - 2}$的图象是由函数$y=\frac{2}{x}$的图象向右平移______个单位长度得到的;
③ 图象关于点______成中心对称(填点的坐标).

|$x$|…|-2|-1|0|$\frac{1}{2}$|1|$\frac{3}{2}$|2|$\frac{5}{2}$|3|$\frac{7}{2}$|4|5|6|…|
|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|
|$y=\frac{2}{x}$|…|-1|-2|■|4|2|$\frac{4}{3}$|1|$\frac{4}{5}$|$\frac{2}{3}$|$\frac{4}{7}$|$\frac{1}{2}$|$\frac{2}{5}$|$\frac{1}{3}$|…|
|$y=\frac{2}{x - 2}$|…|$-\frac{1}{2}$|$-\frac{2}{3}$|-1|$m$|-2|-4|■|4|2|$\frac{4}{3}$|1|$\frac{2}{3}$|$\frac{1}{2}$|…|
(1) $m=$______.
(2) 请画出函数$y=\frac{2}{x - 2}(x\neq2)$的图象.
(3) 观察图象并分析表格,回答下列问题:
① 当$x<2$时,$y$随$x$的增大而______(填“增大”或“减小”);
② 函数$y=\frac{2}{x - 2}$的图象是由函数$y=\frac{2}{x}$的图象向右平移______个单位长度得到的;
③ 图象关于点______成中心对称(填点的坐标).


答案:
(1)$-\frac{4}{3}$ (2)函数图象如图所示 (3)① 减小 ② 2 ③ (2,0)
(1)$-\frac{4}{3}$ (2)函数图象如图所示 (3)① 减小 ② 2 ③ (2,0)

查看更多完整答案,请扫码查看


