第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
6. 已知反比例函数$y=\frac{2m - 3}{x}$的图象在每个象限内,函数值y随自变量x的增大而增大,则m的取值范围是_______.
答案:
$m<\frac{3}{2}$
7. 对于反比例函数$y=-\frac{10}{x}$,当$y<5$,且$y\neq0$时,x的取值范围是____________.
答案:
$x > 0$或$x < -2$
8. ★★如图,在直角坐标系中,$\square OABC$的顶点C在x轴上,顶点B在第二象限,边BC的中点D的横坐标为-6,反比例函数$y=\frac{k}{x}(x<0)$的图象经过点A,D. 若$S_{\triangle AOD}=9$,则k的值为_______.


答案:
-12 解析:如图,过点D作$DE\perp x$轴,过点A作$AF\perp x$轴,垂足分别为E,F. $\because$边BC的中点D的横坐标为-6,点D在反比例函数$y = \frac{k}{x}(x < 0)$的图象上,$\therefore D(-6,-\frac{k}{6})$,则易得点B的纵坐标为$-\frac{k}{3}$. $\therefore A(-3,-\frac{k}{3})$. 根据反比例函数k的几何意义,得$S_{\triangle DOE}=S_{\triangle AOF}=\frac{1}{2}|k|$,$\therefore S_{\triangle DOE}-S_{\triangle GOF}=S_{\triangle AOF}-S_{\triangle GOF}$,即$S_{四边形DEFG}=S_{\triangle AGO}$. $\therefore S_{四边形DEFG}+S_{\triangle ADG}=S_{\triangle AGO}+S_{\triangle ADG}$,即$S_{梯形ADEF}=S_{\triangle AOD}=9$. $\therefore \frac{1}{2}[-\frac{k}{6}+(-\frac{k}{3})]\times(-3 + 6)=9$,解得$k = -12$.

-12 解析:如图,过点D作$DE\perp x$轴,过点A作$AF\perp x$轴,垂足分别为E,F. $\because$边BC的中点D的横坐标为-6,点D在反比例函数$y = \frac{k}{x}(x < 0)$的图象上,$\therefore D(-6,-\frac{k}{6})$,则易得点B的纵坐标为$-\frac{k}{3}$. $\therefore A(-3,-\frac{k}{3})$. 根据反比例函数k的几何意义,得$S_{\triangle DOE}=S_{\triangle AOF}=\frac{1}{2}|k|$,$\therefore S_{\triangle DOE}-S_{\triangle GOF}=S_{\triangle AOF}-S_{\triangle GOF}$,即$S_{四边形DEFG}=S_{\triangle AGO}$. $\therefore S_{四边形DEFG}+S_{\triangle ADG}=S_{\triangle AGO}+S_{\triangle ADG}$,即$S_{梯形ADEF}=S_{\triangle AOD}=9$. $\therefore \frac{1}{2}[-\frac{k}{6}+(-\frac{k}{3})]\times(-3 + 6)=9$,解得$k = -12$.

9. (24分)(泰安中考)如图,直线$y_1=kx + b$与反比例函数$y_2=-\frac{8}{x}$的图象相交于点$A(-2,m)$,$B(n,-1)$,与y轴交于点C.
(1) 求直线AB对应的函数解析式;
(2) 若$y_1>y_2$,请直接写出满足条件的x的取值范围;
(3) 过点C作x轴的平行线交反比例函数的图象于点D,连接AD,求$\triangle ACD$的面积.
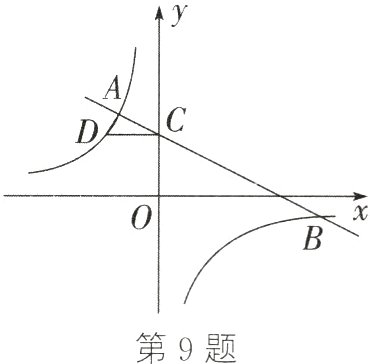
(1) 求直线AB对应的函数解析式;
(2) 若$y_1>y_2$,请直接写出满足条件的x的取值范围;
(3) 过点C作x轴的平行线交反比例函数的图象于点D,连接AD,求$\triangle ACD$的面积.

答案:
(1)将$A(-2,m)$,$B(n,-1)$代入$y_{2}=-\frac{8}{x}$,得$\begin{cases}-2m=-8\\-n=-8\end{cases}$,解得$\begin{cases}m = 4\\n = 8\end{cases}$. $\therefore$点A的坐标为$(-2,4)$,点B的坐标为$(8,-1)$. 把$A(-2,4)$,$B(8,-1)$代入$y_{1}=kx + b$,得$\begin{cases}-2k + b = 4\\8k + b = -1\end{cases}$,解得$\begin{cases}k=-\frac{1}{2}\\b = 3\end{cases}$. $\therefore$直线AB对应的函数解析式为$y_{1}=-\frac{1}{2}x + 3$ (2)由图象可知,当$y_{1}>y_{2}$时,$x < -2$或$0 < x < 8$ (3)在$y_{1}=-\frac{1}{2}x + 3$中,令$x = 0$,则$y_{1}=3$,$\therefore$点C的坐标为$(0,3)$. 在$y_{2}=-\frac{8}{x}$中,令$y_{2}=3$,则$-\frac{8}{x}=3$,解得$x = -\frac{8}{3}$,$\therefore$点D的坐标为$(-\frac{8}{3},3)$. $\therefore CD=\frac{8}{3}$. $\therefore S_{\triangle ACD}=\frac{1}{2}\times\frac{8}{3}\times(4 - 3)=\frac{4}{3}$
10. ★(28分)如图,一次函数$y=x + b$的图象与反比例函数$y=\frac{k}{x}$的图象相交于点$A(m,4)$,与x轴相交于点B,与y轴相交于点$C(0,3)$.
(1) 求m,k的值;
(2) 若D是反比例函数$y=\frac{k}{x}$的图象上一点,且$S_{\triangle OBD}=2S_{\triangle OAC}$,求点D的坐标.

(1) 求m,k的值;
(2) 若D是反比例函数$y=\frac{k}{x}$的图象上一点,且$S_{\triangle OBD}=2S_{\triangle OAC}$,求点D的坐标.

答案:
(1)将$C(0,3)$代入$y = x + b$,得$b = 3$,$\therefore$一次函数的解析式为$y = x + 3$. $\because$点$A(m,4)$在一次函数的图象上,$\therefore m + 3 = 4$,解得$m = 1$. $\therefore A(1,4)$. $\because$点$A(1,4)$在反比例函数的图象上,$\therefore k = 1\times4 = 4$ (2)在$y = x + 3$中,令$y = 0$,则$x + 3 = 0$,解得$x = -3$,$\therefore$点B的坐标为$(-3,0)$. $\therefore OB = 3$. $\because$点C的坐标为$(0,3)$,$\therefore OC = 3$. $\because S_{\triangle OBD}=2S_{\triangle OAC}$,$\therefore \frac{1}{2}OB\cdot|y_{D}|=2\times\frac{1}{2}OC\cdot x_{A}$,即$\frac{1}{2}\times3|y_{D}|=2\times\frac{1}{2}\times3\times1$,解得$y_{D}=\pm2$. $\because D$是反比例函数$y=\frac{4}{x}$的图象上一点,$\therefore$当$y = 2$时,$\frac{4}{x}=2$,解得$x = 2$;当$y = -2$时,$\frac{4}{x}=-2$,解得$x = -2$. 综上所述,点D的坐标为$(2,2)$或$(-2,-2)$
__________
答案:
__________
答案:
查看更多完整答案,请扫码查看


