2026年1号卷中考试题精编九年级数学安徽专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年1号卷中考试题精编九年级数学安徽专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
16. 如图,在由边长为$1$个单位长度的小正方形组成的网格中建立平面直角坐标系$xOy$,格点(网格线的交点)$A$,$B$,$C$,$D$的坐标分别为$(7,8)$,$(2,8)$,$(10,4)$,$(5,4)$.
(1)以点$D$为旋转中心,将$\triangle ABC$旋转$180^{\circ}$得到$\triangle A_{1}B_{1}C_{1}$,画出$\triangle A_{1}B_{1}C_{1}$.
(2)直接写出以$B$,$C_{1}$,$B_{1}$,$C$为顶点的四边形的面积.
(3)在所给的网格图中确定一个格点$E$,使得射线$AE$平分$\angle BAC$,写出点$E$的坐标.
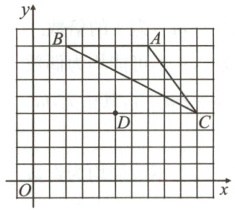
(1)以点$D$为旋转中心,将$\triangle ABC$旋转$180^{\circ}$得到$\triangle A_{1}B_{1}C_{1}$,画出$\triangle A_{1}B_{1}C_{1}$.
(2)直接写出以$B$,$C_{1}$,$B_{1}$,$C$为顶点的四边形的面积.
(3)在所给的网格图中确定一个格点$E$,使得射线$AE$平分$\angle BAC$,写出点$E$的坐标.

答案:
16. 解:
(1)如图,$\triangle A_1B_1C_1$即为所求.(3分)
(2)40.(6分)
(3)$(3,0)$或$(4,2)$或$(5,4)$或$(6,6)$(写出一个即可).(8分)
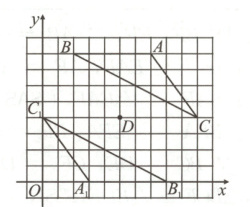
16. 解:
(1)如图,$\triangle A_1B_1C_1$即为所求.(3分)
(2)40.(6分)
(3)$(3,0)$或$(4,2)$或$(5,4)$或$(6,6)$(写出一个即可).(8分)

17. 乡村振兴战略实施以来,很多外出人员返乡创业,某村有部分返乡青年承包了一些田地,采用新技术种植$A$,$B$两种农作物.种植这两种农作物每公顷所需人数和投入资金见下表:

已知农作物种植人员共$24$人,且每人只参与一种农作物种植,投入资金共$60$万元,问$A$,$B$这两种农作物的种植面积各多少公顷?

已知农作物种植人员共$24$人,且每人只参与一种农作物种植,投入资金共$60$万元,问$A$,$B$这两种农作物的种植面积各多少公顷?
答案:
17. 解:设A,B两种农作物的种植面积分别为$x$,$y$公顷. 由题意得,$\begin{cases}4x + 3y = 24, \\8x + 9y = 60,\end{cases}$解得$\begin{cases}x = 3, \\y = 4.\end{cases}$ 答:A,B两种农作物的种植面积分别为3公顷、4公顷.(8分)
18. 数学兴趣小组开展探究活动,研究了“正整数$N$能否表示为$x^{2}-y^{2}$($x$,$y$均为自然数)”的问题.
(1)指导教师将学生的发现进行整理,部分信息如下($n$为正整数):

按上表规律解决下列问题.
(ⅰ)$24=( )^{2}-( )^{2}$.
(ⅱ)$4n=$
(2)兴趣小组还猜测:像$2$,$6$,$10$,$14$,$·s$这些形如$4n-2$($n$为正整数)的正整数$N$不能表示为$x^{2}-y^{2}$($x$,$y$均为自然数).师生一起研讨,分析过程如下:
假设$4n-2=x^{2}-y^{2}$,其中$x$,$y$均为自然数.
分下列三种情形分析.
①若$x$,$y$均为偶数,设$x=2k$,$y=2m$.其中$k$,$m$均为自然数,
则$x^{2}-y^{2}=(2k)^{2}-(2m)^{2}=4(k^{2}-m^{2})$为$4$的倍数.
而$4n-2$不是$4$的倍数,矛盾,故$x$,$y$不可能均为偶数.
②若$x$,$y$均为奇数,设$x=2k+1$,$y=2m+1$,其中$k$,$m$均为自然数,
则$x^{2}-y^{2}=(2k+1)^{2}-(2m+1)^{2}=$
而$4n-2$不是$4$的倍数,矛盾,故$x$,$y$不可能均为奇数.
③若$x$,$y$一个是奇数一个是偶数,则$x^{2}-y^{2}$为奇数.
而$4n-2$是偶数,矛盾,故$x$,$y$不可能一个是奇数一个是偶数.
由①②③可知,猜测正确.
阅读以上内容,请在情形②的横线上填写所缺内容.
(1)指导教师将学生的发现进行整理,部分信息如下($n$为正整数):

按上表规律解决下列问题.
(ⅰ)$24=( )^{2}-( )^{2}$.
(ⅱ)$4n=$
$(n+1)^2-(n-1)^2$
.(2)兴趣小组还猜测:像$2$,$6$,$10$,$14$,$·s$这些形如$4n-2$($n$为正整数)的正整数$N$不能表示为$x^{2}-y^{2}$($x$,$y$均为自然数).师生一起研讨,分析过程如下:
假设$4n-2=x^{2}-y^{2}$,其中$x$,$y$均为自然数.
分下列三种情形分析.
①若$x$,$y$均为偶数,设$x=2k$,$y=2m$.其中$k$,$m$均为自然数,
则$x^{2}-y^{2}=(2k)^{2}-(2m)^{2}=4(k^{2}-m^{2})$为$4$的倍数.
而$4n-2$不是$4$的倍数,矛盾,故$x$,$y$不可能均为偶数.
②若$x$,$y$均为奇数,设$x=2k+1$,$y=2m+1$,其中$k$,$m$均为自然数,
则$x^{2}-y^{2}=(2k+1)^{2}-(2m+1)^{2}=$
$4(k^2-m^2+k-m)$
为$4$的倍数.而$4n-2$不是$4$的倍数,矛盾,故$x$,$y$不可能均为奇数.
③若$x$,$y$一个是奇数一个是偶数,则$x^{2}-y^{2}$为奇数.
而$4n-2$是偶数,矛盾,故$x$,$y$不可能一个是奇数一个是偶数.
由①②③可知,猜测正确.
阅读以上内容,请在情形②的横线上填写所缺内容.
答案:
18. 解:
(1)(ⅰ)7,5.(2分) (ⅱ)$(n + 1)^2 - (n - 1)^2$.(5分)
(2)$4(k^2 - m^2 + k - m)$.(8分)
(1)(ⅰ)7,5.(2分) (ⅱ)$(n + 1)^2 - (n - 1)^2$.(5分)
(2)$4(k^2 - m^2 + k - m)$.(8分)
查看更多完整答案,请扫码查看


