《2026年1号卷中考试题精编九年级数学安徽专版》

18. 为贯彻落实“立德树人”的根本任务,提高学生的劳动素养,某中学拟组织九年级师生去校外劳动教育实践基地参加劳动实践活动,需向某客运公司租客车前往,如表是有关租车的信息:

请根据以上表中的信息,解答下列问题:
(1)客运公司60座和45座的客车每辆每天的租金分别是多少元?
(2)九年级师生到该客运公司租车一天,共需租金多少元?

答案： 18 解：
(1)设 60 座客车每辆每天的租金为 x 元，则 45 座客车每辆每天的租金为(x - 200)元，由题意得，5x + 3(x - 200) = 6200，解得 x = 850，
∴x - 200 = 650，答：60 座客车每辆每天的租金为 850 元，45 座客车每辆每天的租金为 650 元. …………………… (5 分)
(2)由题意得，4 × 850 + 4 × 650 = 6000(元)，答：九年级师生到该客运公司租车一天，共需租金 6000 元. …………………………………… (8 分)

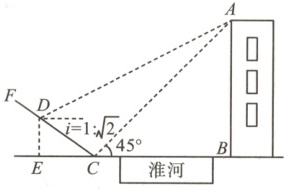
19. 如图,在淮河的右岸边有一座高楼$AB$,左岸有一坡度$i=1:\sqrt{2}$的山坡$CF$,点$C$与点$B$在同一水平面上,$CF$与$AB$在同一平面内.某数学兴趣小组为了测量楼$AB$的高度,在坡底$C$处测得楼顶$A$的仰角为$45^{\circ}$,然后沿坡面$CF$上行了$20\sqrt{3}$米到达点$D$处,点$D$在水平面上的投影为点$E$,此时在$D$处测得楼顶$A$的仰角恰好等于$\angle DCE$,求楼$AB$的高度.(结果保留整数)(参考数据:$\sqrt{2}\approx1.414$)

答案： 19 解：
∵山坡 CF 的坡度 i = 1 : $\sqrt{2}$，设 DE = x 米，则 CE = $\sqrt{2}$x 米，而 CD = 20$\sqrt{3}$米，
∴x² + ($\sqrt{2}$x)² = (20$\sqrt{3}$)²，解得 x = 20，
∴DE = 20 米，CE = 20$\sqrt{2}$米. ……………… (4 分) 如图，过点 D 作 DG ⊥ AB，垂足为 G.
∵△ABC 是等腰直角三角形，设 AB = a 米，则 BC = a 米，AC = $\sqrt{2}$a 米，从而 AG = a - 20，DG = EB = a + 20$\sqrt{2}$，在 Rt△ADG 中，tan∠ADG = $\frac{AG}{DG}$ = tan∠DCE = $\frac{1}{\sqrt{2}}$，即$\frac{a - 20}{a + 20\sqrt{2}}$ = $\frac{1}{\sqrt{2}}$，解得 a = 80 + 40$\sqrt{2}$ ≈ 137，答：楼 AB 的高度约为 137 米. ……………… (10 分)