《2026年1号卷中考试题精编九年级数学安徽专版》

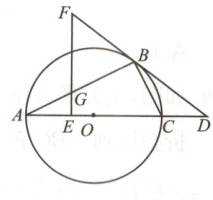
20. 如图,在$Rt\triangle ABC$中,$\angle ABC = 90^{\circ}$,以$AC$为直径作$\odot O$,过点$B$作$\odot O$的切线交$AC$的延长线于点$D$,点$E$在$OA$上,作$EF\perp AC$交$DB$的延长线于点$F$,$EF$与$AB$交于点$G$.
(1)求证:$FG = FB$.
(2)若$\sin D = \frac{3}{5}$,$CD = 2$,$EG = 1$,求$BF$的长.

答案： 20 解：
(1) 证明：如图，连接 $OB$，$\because BD$ 是$\odot O$ 的切线，$\therefore \angle OBF = 90°$，$\therefore \angle OBA + \angle GBF = 90°$，$\because EF \perp AC$，$\therefore \angle AEG = 90°$，$\therefore \angle OAB + \angle EGA = 90°$，又$\because OA = OB$，$\therefore \angle OAB = \angle OBA$，$\therefore \angle GBF = \angle EGA$，又$\because \angle FGB = \angle EGA$，$\therefore \angle GBF = \angle FGB$，$\therefore FG = FB$. ……………… (4 分)
(2)设$\odot O$ 的半径为 $r$，$\because \sin D = \frac{OB}{OD} = \frac{3}{5}$，$\therefore \frac{r}{r + 2} = \frac{3}{5}$，解得 $r = 3$.在 $Rt \triangle OBD$ 中，$BD = \sqrt{OD^2 - OB^2} = \sqrt{5^2 - 3^2} = 4$，$\because \angle D = \angle D$，$\angle OBD = \angle FED = 90°$，$\therefore \triangle DBO \sim \triangle DEF$，$\therefore \frac{EF}{BO} = \frac{FD}{OD}$，即$\frac{FG + GE}{BO} = \frac{FB + BD}{OC + CD}$，得$\frac{BF + 4}{5} = \frac{BF + 1}{3}$，解得 $BF = \frac{7}{2}$. ……………… (10 分)

21. 某校课后延时服务开设多种特色课程,九年级开设的课程主要有:A.播音,B.无人机表演,C.象棋,D.羽毛球,每名同学只能选择一种课程.开学初,班主任对九年级(1)班学生选课情况做了全面调查,根据调查结果绘制了不完整的条形统计图和扇形统计图,请结合图中信息解答下列问题:
(1)求该班学生共有多少名?
(2)求扇形统计图中表示“D课程”的扇形圆心角度数,并补全条形统计图.
(3)已知“A课程”中有2名男同学和3名女同学,学校打算从他们当中选择两名同学担任毕业典礼的主持人,请你用列表或画树状图的方法,求出正好选择一男一女的概率.

答案： 21 解：
(1)$\frac{5}{10\%} = 50 (名)$. ……………… (2 分)
(2)$\frac{50 - (5 + 10 + 15)}{50} × 360° = 144°$；补全的条形统计图如图所示. ……………… (6 分)
(3)画树状图如下：($a$ 表示男生，$b$ 表示女生)
一共有 20 种等可能的情况，其中一男一女的情况有 12 种，$\therefore$ 选中的两名同学是一男一女的概率为 $P_{(一男一女)} = \frac{12}{20} = \frac{3}{5}$. ……………… (12 分)