2026年1号卷中考试题精编九年级数学安徽专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年1号卷中考试题精编九年级数学安徽专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
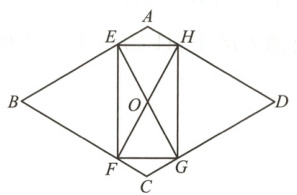
8. 如图,在菱形ABCD中,$AB=2$,$\angle A=120^{\circ}$,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为 (
A.$3+\sqrt{3}$
B.$2+2\sqrt{3}$
C.$2+\sqrt{3}$
D.$1+2\sqrt{3}$
A
)
A.$3+\sqrt{3}$
B.$2+2\sqrt{3}$
C.$2+\sqrt{3}$
D.$1+2\sqrt{3}$
答案:
8 A 【解析】如图,连接BD,AC。
∵四边形ABCD是菱形,∠BAD=120°,
∴AB=BC=CD=AD=2,∠BAO=∠DAO=60°,BD⊥AC,
∴∠ABO=∠CBO=30°,
∴OA=$\frac{1}{2}$AB=1,OB=$\sqrt{3}$OA=$\sqrt{3}$,
∵OE⊥AB,OF⊥BC,BD平分∠ABC,易得OE=OF,BE=BF,又
∵∠EBF=60°,
∴△BEF是等边三角形,
∴EF=BE=$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$,同理可证△DGH,△OEH,△OFG都是等边三角形,
∴EF=GH=$\frac{3}{2}$,EH=FG=$\frac{\sqrt{3}}{2}$,
∴四边形EFGH的周长=3+$\sqrt{3}$。故选A.
∵四边形ABCD是菱形,∠BAD=120°,
∴AB=BC=CD=AD=2,∠BAO=∠DAO=60°,BD⊥AC,
∴∠ABO=∠CBO=30°,
∴OA=$\frac{1}{2}$AB=1,OB=$\sqrt{3}$OA=$\sqrt{3}$,
∵OE⊥AB,OF⊥BC,BD平分∠ABC,易得OE=OF,BE=BF,又
∵∠EBF=60°,
∴△BEF是等边三角形,
∴EF=BE=$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$,同理可证△DGH,△OEH,△OFG都是等边三角形,
∴EF=GH=$\frac{3}{2}$,EH=FG=$\frac{\sqrt{3}}{2}$,
∴四边形EFGH的周长=3+$\sqrt{3}$。故选A.
9. 如图,在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点A的概率是 (

A.$\frac{1}{4}$
B.$\frac{1}{3}$
C.$\frac{3}{8}$
D.$\frac{4}{9}$
D
)
A.$\frac{1}{4}$
B.$\frac{1}{3}$
C.$\frac{3}{8}$
D.$\frac{4}{9}$
答案:
9 D 【解析】由题意知任选两条横线和两条竖线共可以围成9个不同的矩形,其中含点A的矩形有4个,故从这些矩形中任选一个,所选矩形含点A的概率是$\frac{4}{9}$。故选D.
10. 在$\triangle ABC$中,$\angle ACB=90^{\circ}$,分别过点B,C作$\angle BAC$平分线的垂线,垂足分别为点D,E,BC的中点是M,连接CD,MD,ME.则下列结论错误的是 (
A.$CD=2ME$
B.$ME// AB$
C.$BD=CD$
D.$ME=MD$
A
)A.$CD=2ME$
B.$ME// AB$
C.$BD=CD$
D.$ME=MD$
答案:
10 A 【解析】根据题意可作出图形如下:
| 选项 | 分析 | 结论是否正确 |
| --- | --- | --- |
| B | 如图,延长CE交AB于点F。
∵AE平分∠BAC,
∴∠CAE=∠FAE,又
∵∠AEC=∠AEF=90°,AE=AE,
∴△ACE≌△AFE,
∴CE=FE。又
∵点M是BC的中点,
∴EM是△BCF的中位线,
∴EM//BF,即EM//AB。 | 是 |
| C |
∵∠ACB=∠ADB=90°,
∴AB的中点到点A,C,D,B的距离相等,即四边形ACDB有外接圆。由∠CAD=∠BAD,易得∠CAD与∠DAB在四边形ACDB的外接圆中所对的弧相等,
∴CD=BD。 | 是 |
| D | 如图,延长EM交BD于点G。易知CE//BD,
∴∠ECM=∠GBM。又∠CME=∠BMG,CM=BM,
∴△CEM≌△BGM,
∴EM=GM,
∴DM是Rt△EDG斜边EG上的中线,
∴EM=DM。 | 是 |
| A | 仅当∠DCM=30°时,CD=2DM=2ME,此时∠CAB=60°,而题中∠CAB的度数不确定。 | 否 |
一题多解:如图,延长CE交AB于点N,延长AC,BD交于点P。
∵CE⊥AD,BD⊥AD,
∴CN//PB,
∴$\frac{AC}{CP}=\frac{AN}{NB}$。
∵AD平分∠BAC,易得△ACE≌△ANE,△APD≌△ABD,
∴AP=AB,AC=AN,CE=EN,PD=BD,
∴BN=CP。
∵M是BC的中点,
∴EM是△CBN的中位线,DM是△BCP的中位线,
∴EM=$\frac{1}{2}$BN,DM=$\frac{1}{2}$CP,EM//AB,
∴EM=DM,故选项B,D正确。
∵∠ACB=90°,
∴∠BCP=90°,
∵BD=PD,
∴$\frac{1}{2}$BP=BD,故选项C正确。仅当∠DCM=30°时,CD=2DM=2ME,此时∠CAB=60°,而题中∠CAB的度数不确定,故选项A错误,故选A。
| 选项 | 分析 | 结论是否正确 |
| --- | --- | --- |
| B | 如图,延长CE交AB于点F。
∵AE平分∠BAC,
∴∠CAE=∠FAE,又
∵∠AEC=∠AEF=90°,AE=AE,
∴△ACE≌△AFE,
∴CE=FE。又
∵点M是BC的中点,
∴EM是△BCF的中位线,
∴EM//BF,即EM//AB。 | 是 |
| C |
∵∠ACB=∠ADB=90°,
∴AB的中点到点A,C,D,B的距离相等,即四边形ACDB有外接圆。由∠CAD=∠BAD,易得∠CAD与∠DAB在四边形ACDB的外接圆中所对的弧相等,
∴CD=BD。 | 是 |
| D | 如图,延长EM交BD于点G。易知CE//BD,
∴∠ECM=∠GBM。又∠CME=∠BMG,CM=BM,
∴△CEM≌△BGM,
∴EM=GM,
∴DM是Rt△EDG斜边EG上的中线,
∴EM=DM。 | 是 |
| A | 仅当∠DCM=30°时,CD=2DM=2ME,此时∠CAB=60°,而题中∠CAB的度数不确定。 | 否 |
一题多解:如图,延长CE交AB于点N,延长AC,BD交于点P。
∵CE⊥AD,BD⊥AD,
∴CN//PB,
∴$\frac{AC}{CP}=\frac{AN}{NB}$。
∵AD平分∠BAC,易得△ACE≌△ANE,△APD≌△ABD,
∴AP=AB,AC=AN,CE=EN,PD=BD,
∴BN=CP。
∵M是BC的中点,
∴EM是△CBN的中位线,DM是△BCP的中位线,
∴EM=$\frac{1}{2}$BN,DM=$\frac{1}{2}$CP,EM//AB,
∴EM=DM,故选项B,D正确。
∵∠ACB=90°,
∴∠BCP=90°,
∵BD=PD,
∴$\frac{1}{2}$BP=BD,故选项C正确。仅当∠DCM=30°时,CD=2DM=2ME,此时∠CAB=60°,而题中∠CAB的度数不确定,故选项A错误,故选A。
11. 计算:$\sqrt{4}+(-1)^{0}=$
3
.
答案:
11 3
12. 埃及胡夫金字塔是古代世界建筑奇迹之一,其底面是正方形,侧面是全等的等腰三角形.底面正方形的边长与侧面等腰三角形底边上的高的比值是$\sqrt{5}-1$,它介于整数$n$和$n+1$之间,则$n$的值是
1
.
答案:
12 1
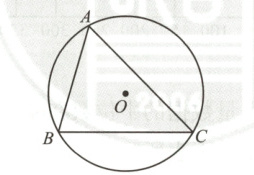
13. 如图,圆O的半径为1,$\triangle ABC$内接于圆O.若$\angle A=60^{\circ}$,$\angle B=75^{\circ}$,则$AB=$
$\sqrt{2}$
.
答案:
13 $\sqrt{2}$ 【解析】如图,连接OA,OB,在△ABC中,∠BAC=60°,∠ABC=75°,
∴∠ACB=180°−∠BAC−∠ABC=45°,
∴∠AOB=90°,
∵OA=OB,
∴△OAB是等腰直角三角形,
∴AB=$\sqrt{2}$OA=$\sqrt{2}$。
∴∠ACB=180°−∠BAC−∠ABC=45°,
∴∠AOB=90°,
∵OA=OB,
∴△OAB是等腰直角三角形,
∴AB=$\sqrt{2}$OA=$\sqrt{2}$。
14. 设抛物线$y=x^{2}+(a+1)x+a$,其中$a$为实数.
(1) 若抛物线经过点$(-1,m)$,则$m=$
(2) 将抛物线$y=x^{2}+(a+1)x+a$向上平移2个单位,所得抛物线顶点的纵坐标的最大值是
(1) 若抛物线经过点$(-1,m)$,则$m=$
0
.(2) 将抛物线$y=x^{2}+(a+1)x+a$向上平移2个单位,所得抛物线顶点的纵坐标的最大值是
2
.
答案:
14
(1)0(2分)
(2)2(3分)
【解析】
(1)点(−1,m)代入y=x²+(a+1)x+a,得(−1)²+(a+1)×(−1)+a=m,解得m=0。
(2)原抛物线顶点的纵坐标为$\frac{4a−(a+1)^2}{4}=\frac{−a^2+2a−1}{4}=−\frac{1}{4}(a−1)^2$,向上平移2个单位后所得抛物线顶点的纵坐标n=$−\frac{1}{4}(a−1)^2+2$,
∵$−\frac{1}{4}$<0,
∴n的最大值为2。

14
(1)0(2分)
(2)2(3分)
【解析】
(1)点(−1,m)代入y=x²+(a+1)x+a,得(−1)²+(a+1)×(−1)+a=m,解得m=0。
(2)原抛物线顶点的纵坐标为$\frac{4a−(a+1)^2}{4}=\frac{−a^2+2a−1}{4}=−\frac{1}{4}(a−1)^2$,向上平移2个单位后所得抛物线顶点的纵坐标n=$−\frac{1}{4}(a−1)^2+2$,
∵$−\frac{1}{4}$<0,
∴n的最大值为2。

15. 解不等式:$\frac{x-1}{3}-1>0$.
答案:
15 解:去分母,得x−1−3>0,……………… (4分)
移项及合并同类项,得x>4。 ………… (8分)
移项及合并同类项,得x>4。 ………… (8分)
查看更多完整答案,请扫码查看


