《2026年1号卷中考试题精编九年级数学安徽专版》

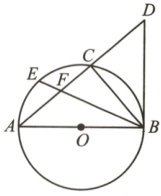
20. 如图，已知$\triangle ABC$内接于$\odot O$，$AB$为直径，过点$B$作$\odot O$的切线交$AC$延长线于$D$，$E$为$\overgroup{AC}$上的一点，连接$BE$，交$AC$于$F$，且$DB=DF$。
（1）求证：$\overgroup{AE}=\overgroup{CE}$。
（2）若$\odot O$的半径为5，$AC=8$，求$CF$的长。

答案： 解：
(1)证明：由题意得，$\angle ACB = \angle ABD = 90°$，$\therefore \angle A = \angle DBC = 90° - \angle D$，$\because DB = DF$，$\therefore \angle DBF = \angle DFB$，$\because \angle DFB = \angle A + \angle ABE$，$\angle DFB = \angle DBC + \angle CBE$，$\therefore \angle ABE = \angle CBE$，$\therefore \overset{\frown} {AE} = \overset{\frown} {CE}$. ………………… (4分)
(2)如图，作 FG⊥AB 于点 G，由题意得，$\angle ACB = 90°$，$AB = 10$，$\because AC = 8$，$\therefore BC = \sqrt{10^{2} - 8^{2}} = 6$，由
(1)知$\angle ABE = \angle CBE$，$\therefore FG = FC$. $\because FB = FB$，$\therefore Rt \triangle FBG \cong Rt \triangle FBC(HL)$，$\therefore BG = BC = 6$. 设$FG = FC = x$，$\therefore AG = AB - BG = 4$，$AF = AC - CF = 8 - x$，在$Rt \triangle AFG$中，由勾股定理得$FG^{2} + AG^{2} = AF^{2}$，即$x^{2} + 4^{2} = (8 - x)^{2}$，解得$x = 3$，$\therefore CF = 3$. ………………… (10分)
思路点拨：
(1)根据圆周角定理和切线的性质得到$\angle ACB = \angle ABD = 90°$，利用等角的余角相等可得$\angle ABE = \angle CBE$，即可证明$\overset{\frown} {AE} = \overset{\frown} {CE}$.
(2)作 FG⊥AB 于点 G，利用角平分线的性质可得$FG = FC$，证明$Rt \triangle FBG \cong Rt \triangle FBC(HL)$，可得$BG = BC = 6$，设$FG = FC = x$，在$Rt \triangle AFG$中，由勾股定理列式计算即可求解.

21. 某校初三年级两个班要举行团体操比赛。两个班各选择8名选手，统计了他们的身高(单位：$cm$)，数据整理如下：
【数据收集与整理】每班8名选手的具体身高：

【数据分析与应用】每班8名选手身高的平均数、中位数、众数如下：

根据以上信息，回答下列问题。
(1)$m=$175，$n=$176。
(2)请计算1班8名选手身高的方差为22.25，2班8名选手身高的方差为26.25，据此推断：在1班和2班的选手中，身高比较整齐的是1班(填“1”或“2”)。
(3)现要从每班的8名选手中分别选出6位选手，1班的6位选手的身高分别为171，172，174，174，176，177。如果2班已经选出的5位选手身高分别为171，174，176，176，178，要使得2班6位选手的平均身高高于1班6位选手的平均身高，且使得本班选手身高比较整齐，则2班需选出的第6位选手的身高是170$cm$。

答案： 解：
(1)2 班数据从小到大排列为 169,170,171，174,176,176,178,186，从中可以看出一共八个数，第四个数据为 174，第五个数据为 176，$\therefore$这组数据的中位数为$(174 + 176) ÷ 2 = 175$，$\therefore m = 175$. 其中 176 出现的次数最多，$\therefore$这组数的众数为 176，$\therefore n = 176$. 故答案为 175,176. …………………………………………… (4分)
(2)1 班的方差为：$\frac{1}{8} × [(170 - 175)^{2} + (171 - 175)^{2} + (172 - 175)^{2} + 2 × (174 - 175)^{2} + (176 - 175)^{2} + (177 - 175)^{2} + (178 - 175)^{2} + (186 - 175)^{2}] = 22.25$.
2 班的方差为：$\frac{1}{8} × [(169 - 175)^{2} + (170 - 175)^{2} + (171 - 175)^{2} + (174 - 175)^{2} + 2 × (176 - 175)^{2} + (178 - 175)^{2} + (186 - 175)^{2}] = 26.25$，根据方差的定义可以知道，方差越大，一组数据的波动越大，稳定性也越小，反之亦然. 据此推断：在 1 班和 2 班的选手中，身高比较整齐的是 1 班. 故答案为 22.25,26.25,1， ……………………… (9分)
(3)$(171 + 172 + 174 + 174 + 176 + 176 + 178) ÷ 6 = 174$（厘米），设 2 班第 6 位选手的身高为$x$厘米，则$(171 + 174 + 176 + 176 + 178 + x) ÷ 6 ＞ 174$，解得$x ＞ 169$，据此，第 6 位可选的人员身高为 170,186，若为 170 时，2 班的身高数据分布于 170～178；若为 186 时，2 班的身高数据分布于 171～186，从中可以看出当身高为 170 时的数据波动更小，更加稳定，$\therefore$第 6 位选手的身高应该是 170 厘米，故答案为 170. …………………………………………… (12分)
方法技巧：统计中“三数一差”的计算方法：将一组数据按照从小到大(或从大到小)的顺序排列，如果这组数据的个数是奇数，则处于中间位置的数为这组数据的中位数，如果这组数据的个数是偶数，则中间位置的两个数据的平均数为这组数据的中位数. 众数是一组数据中出现次数最多的数. 算术平均数的计算公式为$\bar{x} = \frac{1}{n}(x_{1} + x_{2} + ·s + x_{n})$，加权平均数的计算公式为$\bar{x} = \frac{x_{1} · f_{1} + x_{2} · f_{2} + ·s + x_{n} · f_{n}}{f_{1} + f_{2} + ·s + f_{n}}$. 方差$s^{2} = \frac{1}{n}[(x_{1} - \bar{x})^{2} + (x_{2} - \bar{x})^{2} + ·s + (x_{n} - \bar{x})^{2}]$.