2026年1号卷中考试题精编九年级数学安徽专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年1号卷中考试题精编九年级数学安徽专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
9. 在同一平面直角坐标系中,一次函数$y=ax+a^{2}$与$y=a^{2}x+a$的图象可能是 (
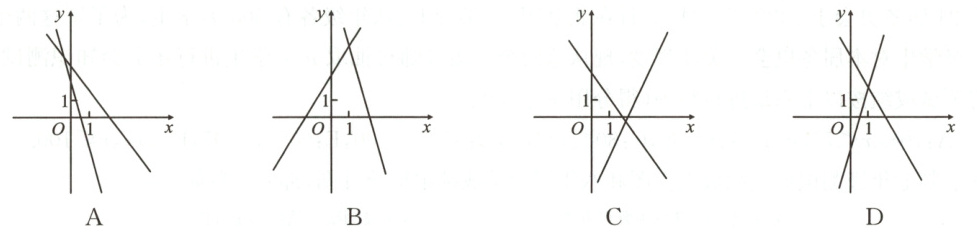
D
)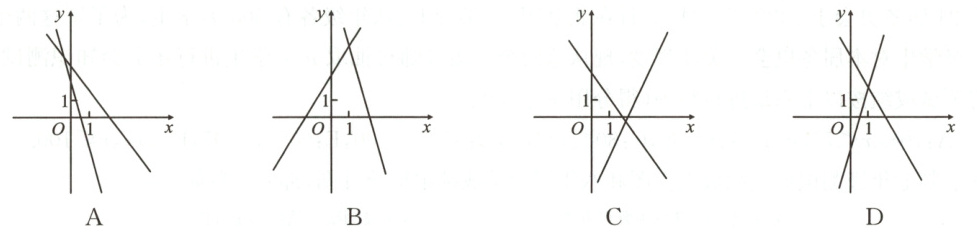
答案:
D 【解析】当$x=1$时,两个函数的函数值都是$a^2+a$,$\therefore$两直线的交点的横坐标为1,可排除A、C选项;若$a>0$,则两直线都经过第一、二、三象限,此时B、D选项都不符合;若$a<0$,则直线$y=ax+a^2$经过第一、二、四象限,D选项符合.故选D.
10. 已知点$O$是边长为6的等边$\triangle ABC$的中心,点$P$在$\triangle ABC$外,$\triangle ABC$,$\triangle PAB$,$\triangle PBC$,$\triangle PCA$的面积分别记为$S_{0}$,$S_{1}$,$S_{2}$,$S_{3}$.若$S_{1}+S_{2}+S_{3}=2S_{0}$,则线段$OP$长的最小值是 (
A.$\frac{3\sqrt{3}}{2}$
B.$\frac{5\sqrt{3}}{2}$
C.$3\sqrt{3}$
D.$\frac{7\sqrt{3}}{2}$
B
)A.$\frac{3\sqrt{3}}{2}$
B.$\frac{5\sqrt{3}}{2}$
C.$3\sqrt{3}$
D.$\frac{7\sqrt{3}}{2}$
答案:
B 【解析】不妨假设点$P$在$AB$的左侧,$\because S_{\triangle PAB}+S_{\triangle ABC}=S_{\triangle PBC}+S_{\triangle PAC}$,$\therefore S_1+S_0=S_2+S_3$,$\because S_1+S_2+S_3=2S_0$,$\therefore S_1+S_0=2S_0$,$\therefore S_1=\frac{1}{2}S_0$,$\because\triangle ABC$是等边三角形,边长为6,$\therefore S_0=\frac{\sqrt{3}}{4}×6^2=9\sqrt{3}$,$\therefore S_1=\frac{9\sqrt{3}}{2}$.过点$P$作$AB$的平行线$PM$,连接$CO$并延长交$AB$于点$R$,交$PM$于点$T$.$\because\triangle PAB$的面积是定值,$\therefore$点$P$的运动轨迹是直线$PM$,$\because O$是$\triangle ABC$的中心,$\therefore CT\perp AB$,$CT\perp PM$,$\frac{1}{2}· AB· RT=\frac{9\sqrt{3}}{2}$,$CR=3\sqrt{3}$,$OR=\sqrt{3}$,$\therefore RT=\frac{3\sqrt{3}}{2}$,$\therefore OT=OR+RT=\frac{5\sqrt{3}}{2}$,$\because OP\geq OT$,$\therefore OP$的最小值为$\frac{5\sqrt{3}}{2}$.当点$P$在区域②时,同理可得$OP$的最小值为$\frac{7\sqrt{3}}{2}$.
如图,当点$P$在区域①③⑤时,$OP$的最小值为$\frac{5\sqrt{3}}{2}$,当点$P$在区域②④⑥时,最小值为$\frac{7\sqrt{3}}{2}$,$\because\frac{5\sqrt{3}}{2}<\frac{7\sqrt{3}}{2}$.故选B.
B 【解析】不妨假设点$P$在$AB$的左侧,$\because S_{\triangle PAB}+S_{\triangle ABC}=S_{\triangle PBC}+S_{\triangle PAC}$,$\therefore S_1+S_0=S_2+S_3$,$\because S_1+S_2+S_3=2S_0$,$\therefore S_1+S_0=2S_0$,$\therefore S_1=\frac{1}{2}S_0$,$\because\triangle ABC$是等边三角形,边长为6,$\therefore S_0=\frac{\sqrt{3}}{4}×6^2=9\sqrt{3}$,$\therefore S_1=\frac{9\sqrt{3}}{2}$.过点$P$作$AB$的平行线$PM$,连接$CO$并延长交$AB$于点$R$,交$PM$于点$T$.$\because\triangle PAB$的面积是定值,$\therefore$点$P$的运动轨迹是直线$PM$,$\because O$是$\triangle ABC$的中心,$\therefore CT\perp AB$,$CT\perp PM$,$\frac{1}{2}· AB· RT=\frac{9\sqrt{3}}{2}$,$CR=3\sqrt{3}$,$OR=\sqrt{3}$,$\therefore RT=\frac{3\sqrt{3}}{2}$,$\therefore OT=OR+RT=\frac{5\sqrt{3}}{2}$,$\because OP\geq OT$,$\therefore OP$的最小值为$\frac{5\sqrt{3}}{2}$.当点$P$在区域②时,同理可得$OP$的最小值为$\frac{7\sqrt{3}}{2}$.
如图,当点$P$在区域①③⑤时,$OP$的最小值为$\frac{5\sqrt{3}}{2}$,当点$P$在区域②④⑥时,最小值为$\frac{7\sqrt{3}}{2}$,$\because\frac{5\sqrt{3}}{2}<\frac{7\sqrt{3}}{2}$.故选B.

11. 不等式$\frac{x-3}{2}\geq1$的解集为
$x\geq5$
.
答案:
$x\geq5$
12. 若一元二次方程$2x^{2}-4x+m=0$有两个相等的实数根,则$m=$
2
$$.
答案:
2
13. 如图,$□ OABC$的顶点$O$是坐标原点,$A$在$x$轴的正半轴上,$B$,$C$在第一象限,反比例函数$y=\frac{1}{x}$的图象经过点$C$,$y=\frac{k}{x}(k\neq0)$的图象经过点$B$.若$OC=AC$,则$k=$
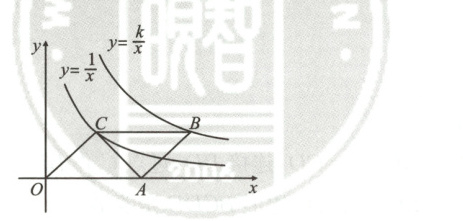
3
$$.
答案:
3
14. 如图,四边形$ABCD$是正方形,点$E$在边$AD$上,$\triangle BEF$是以$E$为直角顶点的等腰直角三角形,$EF$,$BF$分别交$CD$于点$M$,$N$,过点$F$作$AD$的垂线交$AD$的延长线于点$G$.连接$DF$,请解决下列问题.
(1) $\angle FDG=$
(2) 若$DE=1$,$DF=2\sqrt{2}$,则$MN=$
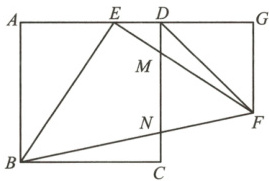
(1) $\angle FDG=$
45
$^{\circ}$.(2) 若$DE=1$,$DF=2\sqrt{2}$,则$MN=$
$\frac{26}{15}$
$$.
答案:
14
(1)45(2分)
(2)$\frac{26}{15}$(3分)
【解析】
(1)由题知,$\triangle BEF$是以$E$为直角顶点的等腰直角三角形,$\therefore\angle AEB+\angle GEF=90°$,$\because\angle AEB+\angle ABE=90°$,$\therefore\angle GEF=\angle ABE$,在$\triangle ABE$和$\triangle GEF$中,$\begin{cases}\angle GEF=\angle ABE\\\angle A=\angle G=90°\\BE=EF\end{cases}$,$\therefore\triangle ABE\cong\triangle GEF$(AAS).$\therefore EG=AB=AD$,$GF=AE$,即$DG+DE=AE+DE$,$\therefore DG=AE$,$\therefore DG=GF$,即$\triangle DGF$是等腰直角三角形,$\therefore\angle FDG=45°$.
(2)$\because DE=1$,$DF=2\sqrt{2}$,由
(1)知,$\triangle DGF$是等腰直角三角形,$\therefore DG=GF=2$,$\therefore AB=AD=CD=ED+DG=2+1=3$.如图,延长$GF$交$BC$延长线于点$H$,易得$CD// GH$,$\therefore\triangle EDM\sim\triangle EGF$,$\therefore\frac{MD}{GF}=\frac{ED}{EG}$,即$\frac{MD}{2}=\frac{1}{3}$,$\therefore MD=\frac{2}{3}$.同理$\triangle BNC\sim\triangle BFH$,$\therefore\frac{NC}{FH}=\frac{BC}{BH}$,即$\frac{NC}{GH - GF}=\frac{BC}{BC + CH}$,$\because\frac{NC}{3 - 2}=\frac{3}{3 + 2}$,$\therefore NC=\frac{3}{5}$,$\therefore MN=CD - MD - NC=3-\frac{2}{3}-\frac{3}{5}=\frac{26}{15}$.
14
(1)45(2分)
(2)$\frac{26}{15}$(3分)
【解析】
(1)由题知,$\triangle BEF$是以$E$为直角顶点的等腰直角三角形,$\therefore\angle AEB+\angle GEF=90°$,$\because\angle AEB+\angle ABE=90°$,$\therefore\angle GEF=\angle ABE$,在$\triangle ABE$和$\triangle GEF$中,$\begin{cases}\angle GEF=\angle ABE\\\angle A=\angle G=90°\\BE=EF\end{cases}$,$\therefore\triangle ABE\cong\triangle GEF$(AAS).$\therefore EG=AB=AD$,$GF=AE$,即$DG+DE=AE+DE$,$\therefore DG=AE$,$\therefore DG=GF$,即$\triangle DGF$是等腰直角三角形,$\therefore\angle FDG=45°$.
(2)$\because DE=1$,$DF=2\sqrt{2}$,由
(1)知,$\triangle DGF$是等腰直角三角形,$\therefore DG=GF=2$,$\therefore AB=AD=CD=ED+DG=2+1=3$.如图,延长$GF$交$BC$延长线于点$H$,易得$CD// GH$,$\therefore\triangle EDM\sim\triangle EGF$,$\therefore\frac{MD}{GF}=\frac{ED}{EG}$,即$\frac{MD}{2}=\frac{1}{3}$,$\therefore MD=\frac{2}{3}$.同理$\triangle BNC\sim\triangle BFH$,$\therefore\frac{NC}{FH}=\frac{BC}{BH}$,即$\frac{NC}{GH - GF}=\frac{BC}{BC + CH}$,$\because\frac{NC}{3 - 2}=\frac{3}{3 + 2}$,$\therefore NC=\frac{3}{5}$,$\therefore MN=CD - MD - NC=3-\frac{2}{3}-\frac{3}{5}=\frac{26}{15}$.

查看更多完整答案,请扫码查看


