2026年1号卷中考试题精编九年级数学安徽专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年1号卷中考试题精编九年级数学安徽专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
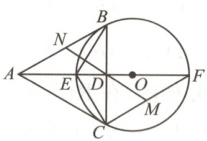
20. 如图,在$\triangle ABC$中,$AB=AC$,$D$是$BC$的中点,$\angle ABC$的平分线交$AD$于点$E$.点$O$在$AD$的延长线上,以$O$为圆心,$OE$为半径的$\odot O$经过点$B,C$.
(1)若$AB=2\sqrt{3}$,$BD=\sqrt{3}$,求$\odot O$的半径.
(2)设$\odot O$与$AD$的延长线交于点$F$,$M$是$CF$的中点,$MD$的延长线与$AB$交于点$N$.求证:$BN=BD$.
(1)若$AB=2\sqrt{3}$,$BD=\sqrt{3}$,求$\odot O$的半径.
(2)设$\odot O$与$AD$的延长线交于点$F$,$M$是$CF$的中点,$MD$的延长线与$AB$交于点$N$.求证:$BN=BD$.

答案:
20 解:
(1)如图,连接 OB,设⊙O 的半径为 R,
∵在△ABC 中,AB = AC,D 是 BC 的中点,
∴AD ⊥ BC.在 Rt△ABD 中,AB = 2$\sqrt{3}$,BD = $\sqrt{3}$,
∴sin∠BAD = $\frac{BD}{AB}$ = $\frac{\sqrt{3}}{2\sqrt{3}}$ = $\frac{1}{2}$,
∴∠BAD = 30°,
∴∠ABC = 90° - ∠BAD = 60°.
∵BE 是∠ABD 的平分线,
∴∠ABE = $\frac{1}{2}$∠ABC = 30°,
∴∠ABE = ∠BAD = 30°,
∴AE = BE,∠BEO = ∠ABE + ∠BAD = 60°.
∵点 O 是⊙O 的圆心,OE 为半径,⊙O 经过点 B、C,
∴OB = OE,又
∵∠BEO = 60°,
∴△OBE 是等边三角形,
∴∠OBE = 60°,OB = OE = BE = R,
∴AE = BE = R,
∴OA = OE + AE = 2R,
∵∠ABO = ∠ABE + ∠OBE = 30° + 60° = 90°,
∴△AOB 是直角三角形,在 Rt△AOB 中,由勾股定理得 OA² = AB² + OB²,
∴(2$\sqrt{3}$)² + R² = (2R)²,解得 R = 2(负值舍去),
∴⊙O 的半径为 2. ………………………… (5 分)
(2)证明:在 Rt△CDF 中,M 是 CF 的中点,
∴MD = MC = MF,
∴∠MDF = ∠F.
∵∠F = ∠DBE,∠MDF = ∠ADN,
∴∠DBE = ∠ADN,
∵AD ⊥ BC,
∴∠ADN + ∠BDN = 90°,
∴∠DBE + ∠BDN = 90°,
∴BE ⊥ ND.又
∵BE 是∠ABD 的平分线,
∴∠BND = ∠BDN,
∴BN = BD. ………… (10 分)
(1)如图,连接 OB,设⊙O 的半径为 R,
∵在△ABC 中,AB = AC,D 是 BC 的中点,
∴AD ⊥ BC.在 Rt△ABD 中,AB = 2$\sqrt{3}$,BD = $\sqrt{3}$,
∴sin∠BAD = $\frac{BD}{AB}$ = $\frac{\sqrt{3}}{2\sqrt{3}}$ = $\frac{1}{2}$,
∴∠BAD = 30°,
∴∠ABC = 90° - ∠BAD = 60°.
∵BE 是∠ABD 的平分线,
∴∠ABE = $\frac{1}{2}$∠ABC = 30°,
∴∠ABE = ∠BAD = 30°,
∴AE = BE,∠BEO = ∠ABE + ∠BAD = 60°.
∵点 O 是⊙O 的圆心,OE 为半径,⊙O 经过点 B、C,
∴OB = OE,又
∵∠BEO = 60°,
∴△OBE 是等边三角形,
∴∠OBE = 60°,OB = OE = BE = R,
∴AE = BE = R,
∴OA = OE + AE = 2R,
∵∠ABO = ∠ABE + ∠OBE = 30° + 60° = 90°,
∴△AOB 是直角三角形,在 Rt△AOB 中,由勾股定理得 OA² = AB² + OB²,
∴(2$\sqrt{3}$)² + R² = (2R)²,解得 R = 2(负值舍去),
∴⊙O 的半径为 2. ………………………… (5 分)
(2)证明:在 Rt△CDF 中,M 是 CF 的中点,
∴MD = MC = MF,
∴∠MDF = ∠F.
∵∠F = ∠DBE,∠MDF = ∠ADN,
∴∠DBE = ∠ADN,
∵AD ⊥ BC,
∴∠ADN + ∠BDN = 90°,
∴∠DBE + ∠BDN = 90°,
∴BE ⊥ ND.又
∵BE 是∠ABD 的平分线,
∴∠BND = ∠BDN,
∴BN = BD. ………… (10 分)
21. 综合与实践
【项目背景】
安全防范教育是培养学生健康成长的重要环节,提高学生的安全意识,使其具备安全知识和自我救护能力,养成良好的安全行为习惯,对于保障学生的人身安全和营造平安和谐的校园环境有重要意义.某校为加强安全教育,开展了“防溺水”安全知识检测.
【数据收集与整理】
某校七、八年级各有1000名学生,现从七、八年级学生中各随机抽取了$m$名学生进行测试,将各年级测试成绩按如表分组方式分成6个组(得分用$x$表示):

绘制七年级测试成绩频数直方图和八年级测试成绩扇形统计图,部分信息如下:
七年级测试成绩频数直方图 八年级测试成绩扇形统计图
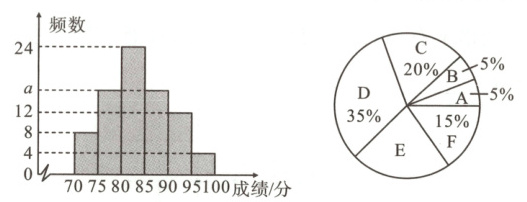
已知八年级测试成绩$B$组的全部数据为75,77,78,79.
【数据分析与运用】
根据以上信息,完成以下任务:
任务1 $m=$
任务2 请直接写出七年级测试成绩的中位数落在哪一组.
任务3 若测试成绩不低于85分,则认定该学生对“防溺水”安全知识了解程度高,请估计该校七、八两个年级中,哪个年级对“防溺水”安全知识了解程度更高一些,并说明理由.
【项目背景】
安全防范教育是培养学生健康成长的重要环节,提高学生的安全意识,使其具备安全知识和自我救护能力,养成良好的安全行为习惯,对于保障学生的人身安全和营造平安和谐的校园环境有重要意义.某校为加强安全教育,开展了“防溺水”安全知识检测.
【数据收集与整理】
某校七、八年级各有1000名学生,现从七、八年级学生中各随机抽取了$m$名学生进行测试,将各年级测试成绩按如表分组方式分成6个组(得分用$x$表示):

绘制七年级测试成绩频数直方图和八年级测试成绩扇形统计图,部分信息如下:
七年级测试成绩频数直方图 八年级测试成绩扇形统计图

已知八年级测试成绩$B$组的全部数据为75,77,78,79.
【数据分析与运用】
根据以上信息,完成以下任务:
任务1 $m=$
80
$$,$a=$16
$$.任务2 请直接写出七年级测试成绩的中位数落在哪一组.
任务3 若测试成绩不低于85分,则认定该学生对“防溺水”安全知识了解程度高,请估计该校七、八两个年级中,哪个年级对“防溺水”安全知识了解程度更高一些,并说明理由.
答案:
21 解:任务 1 依题意,m = 4 ÷ 5% = 80,
∴a = 80 - 8 - 24 - 12 - 4 - a,
∴a = 16,故答案为 80,16. …………………………… (4 分) 任务 2 8 + 16 = 24 < 40,8 + 16 + 24 = 48 > 41,
∴中位数落在 80 ≤ x < 85,即 C 组. ………… (8 分) 任务 3 七年级测试成绩不低于 85 分的有 16 + 12 + 4 = 32(人),
∴$\frac{32}{80}$ × 100% = 40%,八年级测试成绩不低于 85 分的有 1 - (20% + 5% + 5%) = 70%,
∵40% < 70%,且两个年级学生数和抽取的学生数均相同,
∴八年级对“防溺水”安全知识了解程度更高一些. …………………………………………… (12 分)
∴a = 80 - 8 - 24 - 12 - 4 - a,
∴a = 16,故答案为 80,16. …………………………… (4 分) 任务 2 8 + 16 = 24 < 40,8 + 16 + 24 = 48 > 41,
∴中位数落在 80 ≤ x < 85,即 C 组. ………… (8 分) 任务 3 七年级测试成绩不低于 85 分的有 16 + 12 + 4 = 32(人),
∴$\frac{32}{80}$ × 100% = 40%,八年级测试成绩不低于 85 分的有 1 - (20% + 5% + 5%) = 70%,
∵40% < 70%,且两个年级学生数和抽取的学生数均相同,
∴八年级对“防溺水”安全知识了解程度更高一些. …………………………………………… (12 分)
查看更多完整答案,请扫码查看


