2026年1号卷中考试题精编九年级数学安徽专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年1号卷中考试题精编九年级数学安徽专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
7. 寿县古城位于安徽省淮南市,淮河南岸,依八公山. 寿县古城始建于宋朝(1068-1224 年),是棋盘式布局的一座宋城. 寿县古城有东门“宾阳门”,南门“通淝门”,西门“定湖门”,北门“靖淮门”四个城门供游客出人,某个周末小浩、小凡在寿县古城内游玩,游玩结束后,他们随机地从其中一个城门离开,则他们恰好从同一个城门出城的概率是 (
A.$\frac{1}{2}$
B.$\frac{1}{4}$
C.$\frac{1}{8}$
D.$\frac{1}{16}$
B
)A.$\frac{1}{2}$
B.$\frac{1}{4}$
C.$\frac{1}{8}$
D.$\frac{1}{16}$
答案:
7 B 【解析】将四个城门分别记为$A$,$B$,$C$,$D$,列表如下:
| | A | B | C | D |
| --- | --- | --- | --- | --- |
| A | (A,A) | (A,B) | (A,C) | (A,D) |
| B | (B,A) | (B,B) | (B,C) | (B,D) |
| C | (C,A) | (C,B) | (C,C) | (C,D) |
| D | (D,A) | (D,B) | (D,C) | (D,D) |
共有16种等可能的结果,其中他们恰好从同一个城门出城的结果有4种,
∴他们恰好从同一个城门出城的概率为$\frac{4}{16}=\frac{1}{4}$。故选B。
| | A | B | C | D |
| --- | --- | --- | --- | --- |
| A | (A,A) | (A,B) | (A,C) | (A,D) |
| B | (B,A) | (B,B) | (B,C) | (B,D) |
| C | (C,A) | (C,B) | (C,C) | (C,D) |
| D | (D,A) | (D,B) | (D,C) | (D,D) |
共有16种等可能的结果,其中他们恰好从同一个城门出城的结果有4种,
∴他们恰好从同一个城门出城的概率为$\frac{4}{16}=\frac{1}{4}$。故选B。
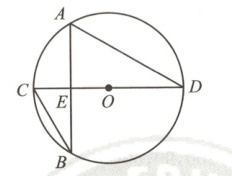
8. 如图,$CD$为$\odot O$的直径,弦$AB$交$CD$于点$E$,点$C$为$AB$中点,若$\overset{\frown}{BC}$的度数为$60^{\circ}$,点$O$到$AD$的距离为$2$,则$OE$的长为 (
A.$\sqrt{3}$
B.$2\sqrt{3}$
C.$3$
D.$2$
D
)
A.$\sqrt{3}$
B.$2\sqrt{3}$
C.$3$
D.$2$
答案:
8 D 【解析】如图,连接$AO$,过点$O$作$OH \perp AD$于$H$,
∵点$O$到$AD$的距离为2,
∴$OH=2$,
∵$CD$为$\odot O$的直径,$C$为$\widehat{AB}$中点,
∴$CD \perp AB$,
∵$BC$的度数为$60^{\circ}$,$C$为$\widehat{AB}$中点,
∴$\angle AOC=60^{\circ}$,
∴$\angle ODH=\frac{1}{2}\angle AOC=30^{\circ}$,
∵$\angle OHD=90^{\circ}$,
∴$OH=\frac{1}{2}OD$,
∵$\angle OAE=90^{\circ}-60^{\circ}=30^{\circ}$,
∴$OE=\frac{1}{2}OA$,
∵$OA=OD$,
∴$OE=OH=2$。故选D。
∵点$O$到$AD$的距离为2,
∴$OH=2$,
∵$CD$为$\odot O$的直径,$C$为$\widehat{AB}$中点,
∴$CD \perp AB$,
∵$BC$的度数为$60^{\circ}$,$C$为$\widehat{AB}$中点,
∴$\angle AOC=60^{\circ}$,
∴$\angle ODH=\frac{1}{2}\angle AOC=30^{\circ}$,
∵$\angle OHD=90^{\circ}$,
∴$OH=\frac{1}{2}OD$,
∵$\angle OAE=90^{\circ}-60^{\circ}=30^{\circ}$,
∴$OE=\frac{1}{2}OA$,
∵$OA=OD$,
∴$OE=OH=2$。故选D。
9. 已知实数$a,b,c,p,q$其中$a\neq0$,满足$p + q = \frac{b}{a}$,$pq = \frac{c}{a}$. 则以下说法:①$b^{2}-4ac\geqslant0$;②$p,q$是关于$x$的一元二次方程$ax^{2}+bx + c = 0$的两个根;③$|p - q| = \frac{\sqrt{b^{2}-4ac}}{|a|}$;④若$a,b,c$均为奇数,则$p,q$可能都为整数. 其中正确的个数是 (
A.1
B.2
C.3
D.4
B
)A.1
B.2
C.3
D.4
答案:
9 B 【解析】逐个说法分析如下:
| 序号 | 分析 | 说法是否正确 |
| --- | --- | --- |
| ① | $\because p+q=\frac{b}{a},pq=\frac{c}{a},\therefore b=(p+q)a$,$c=pqa,\therefore b^{2}-4ac=[(p+q)a]^{2}-4a× pqa=a^{2}[(p+q)^{2}-4pq]=a^{2}(p-q)^{2}\geq0$。 | 是 |
| ② | $\because p,q$是关于$x$的一元二次方程$ax^{2}+bx+c=0$的两个根,$\therefore p+q=-\frac{b}{a},pq=\frac{c}{a}$,
∴与题中$p+q=\frac{b}{a}$不符。 | 否 |
| ③ | $(p+q)^{2}-4pq=\left(\frac{b}{a}\right)^{2}-4×\frac{c}{a}=\frac{b^{2}-4ac}{a^{2}},\therefore \vert p-q\vert=\frac{\sqrt{b^{2}-4ac}}{\vert a\vert}$。 | 是 |
| ④ | 设$p,q$为整数,当$a,b,c$均为奇数时,则$p+q=\frac{b}{a}$为奇数,即$p,q$一奇一偶;$pq=\frac{c}{a}$为奇数,即$p,q$全为奇数,此时相矛盾。 | 否 |
故选B。
| 序号 | 分析 | 说法是否正确 |
| --- | --- | --- |
| ① | $\because p+q=\frac{b}{a},pq=\frac{c}{a},\therefore b=(p+q)a$,$c=pqa,\therefore b^{2}-4ac=[(p+q)a]^{2}-4a× pqa=a^{2}[(p+q)^{2}-4pq]=a^{2}(p-q)^{2}\geq0$。 | 是 |
| ② | $\because p,q$是关于$x$的一元二次方程$ax^{2}+bx+c=0$的两个根,$\therefore p+q=-\frac{b}{a},pq=\frac{c}{a}$,
∴与题中$p+q=\frac{b}{a}$不符。 | 否 |
| ③ | $(p+q)^{2}-4pq=\left(\frac{b}{a}\right)^{2}-4×\frac{c}{a}=\frac{b^{2}-4ac}{a^{2}},\therefore \vert p-q\vert=\frac{\sqrt{b^{2}-4ac}}{\vert a\vert}$。 | 是 |
| ④ | 设$p,q$为整数,当$a,b,c$均为奇数时,则$p+q=\frac{b}{a}$为奇数,即$p,q$一奇一偶;$pq=\frac{c}{a}$为奇数,即$p,q$全为奇数,此时相矛盾。 | 否 |
故选B。
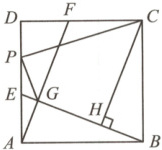
10. 如图,正方形$ABCD$的边长为 8,点$E,P$在边$AD$上运动,点$F$在边$CD$上运动,$ED = CF$,连接$BE,AF$交于点$G$,过点$C$作$CH\perp BE$于点$H$,连接$CP,PG$,下列结论中错误的是 (
A.$AE + BC\geqslant AF$
B.$\triangle AGB$的面积有最大值为 16
C.$CH + AG$有最大值为$8\sqrt{2}$
D.$CP + PG$的最小值为$2\sqrt{13}-4$
D
)
A.$AE + BC\geqslant AF$
B.$\triangle AGB$的面积有最大值为 16
C.$CH + AG$有最大值为$8\sqrt{2}$
D.$CP + PG$的最小值为$2\sqrt{13}-4$
答案:
10 D 【解析】逐项分析如下:
$\because CH \perp BE$,$\therefore \angle HCB + \angle HBC = \angle GBA + \angle HBC = 90^{\circ}$,$\therefore \angle HCB = \angle GBA$,又$\because \angle AGB = \angle BHC = 90^{\circ}$,$AB = BC$,$\therefore \triangle AGB \cong \triangle BHC (AAS)$,$\therefore CH = BG$,$\therefore AG + CH = AG + BG$。设$AG = a$,$BG = b$,在$Rt \triangle ABG$中,由勾股定理得$AG^{2} + BG^{2} = AB^{2}$,
$\therefore a^{2} + b^{2} = 8^{2} = 64$,$\because S_{\triangle ABG} = \frac{1}{2} AG · BG = \frac{1}{2} ab$,$\therefore \frac{1}{2} ab \leq 16$,$\therefore ab \leq 32$,
$\therefore (a + b)^{2} = a^{2} + b^{2} + 2ab \leq 64 + 64 = 128$,$\because a > 0$,$b > 0$,$\therefore a + b \leq 8\sqrt{2}$,
$\therefore AG + BG$的最大值为$8\sqrt{2}$,即$AG + CH$的最大值为$8\sqrt{2}$。
如图,作点$C$关于$AD$的对称点$N$,连接$PN$,$ON$,$\therefore DN = CD = 8$,$PN = PC$,$\therefore CP + PG = NP + PG$,$\therefore$当$N$,$P$,$G$,$O$四点共线时,$NP + PG$有最小值,即此时$CP + PG$有最小值,最小值为$ON - OG$。 如图,过点$O$作$OM \perp CD$于$M$,则四边形$AOMD$是矩形,$\therefore OM = AB = 8$,$DM = OA = \frac{1}{2} AB = 4$,$\therefore MN = DN + DM = 12$,
$\therefore ON = \sqrt{MN^{2} + OM^{2}} = 4\sqrt{13}$,
$\therefore ON - OG = 4\sqrt{13} - 4$,$\therefore CP + PG$的最小值为$4\sqrt{13} - 4$。故选D。
$\because CH \perp BE$,$\therefore \angle HCB + \angle HBC = \angle GBA + \angle HBC = 90^{\circ}$,$\therefore \angle HCB = \angle GBA$,又$\because \angle AGB = \angle BHC = 90^{\circ}$,$AB = BC$,$\therefore \triangle AGB \cong \triangle BHC (AAS)$,$\therefore CH = BG$,$\therefore AG + CH = AG + BG$。设$AG = a$,$BG = b$,在$Rt \triangle ABG$中,由勾股定理得$AG^{2} + BG^{2} = AB^{2}$,
$\therefore a^{2} + b^{2} = 8^{2} = 64$,$\because S_{\triangle ABG} = \frac{1}{2} AG · BG = \frac{1}{2} ab$,$\therefore \frac{1}{2} ab \leq 16$,$\therefore ab \leq 32$,
$\therefore (a + b)^{2} = a^{2} + b^{2} + 2ab \leq 64 + 64 = 128$,$\because a > 0$,$b > 0$,$\therefore a + b \leq 8\sqrt{2}$,
$\therefore AG + BG$的最大值为$8\sqrt{2}$,即$AG + CH$的最大值为$8\sqrt{2}$。
如图,作点$C$关于$AD$的对称点$N$,连接$PN$,$ON$,$\therefore DN = CD = 8$,$PN = PC$,$\therefore CP + PG = NP + PG$,$\therefore$当$N$,$P$,$G$,$O$四点共线时,$NP + PG$有最小值,即此时$CP + PG$有最小值,最小值为$ON - OG$。 如图,过点$O$作$OM \perp CD$于$M$,则四边形$AOMD$是矩形,$\therefore OM = AB = 8$,$DM = OA = \frac{1}{2} AB = 4$,$\therefore MN = DN + DM = 12$,
$\therefore ON = \sqrt{MN^{2} + OM^{2}} = 4\sqrt{13}$,
$\therefore ON - OG = 4\sqrt{13} - 4$,$\therefore CP + PG$的最小值为$4\sqrt{13} - 4$。故选D。
11. 计算:$\sqrt{16} + | -1| =$
5
.
答案:
11 5
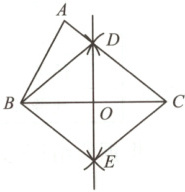
12. 如图,在$\triangle ABC$中,分别以点$B,C$为圆心,大于$\frac{1}{2}BC$的长为半径画弧,两弧交 $B$于点$D,E$,且点$D$恰好在$AC$边上,直线$DE$与$BC$交于点$O$,连接$BD,BE$, $CE$. 若$CD = 5,OD = 3$,则线段$BC$的长为
8
.
答案:
12 8
查看更多完整答案,请扫码查看


