《2026年1号卷中考试题精编九年级数学安徽专版》

8. 新考法·新定义试题 设$x\gt0,y\gt0$,定义新运算:$x\otimes y=\frac{x× y}{x+y}$,若$a\gt0,b\gt0,c\gt0$,则下列式子正确的是 (B)

A.$a\otimes(b× c)=(a\otimes b)× c$
B.$a\otimes(b\otimes c)=(a\otimes b)\otimes c$
C.$a\otimes(b+c)=a\otimes b+a\otimes c$
D.$a×(b\otimes c)=(a× b)\otimes c$

答案： 8 B 【解析】逐项分析如下.故选 B. 选项 分析 正误
∵a⊗(b×c) = $\frac{abc}{a + bc}$，(a⊗b)×c = $\frac{ab}{a + b}$×c = $\frac{abc}{a + b}$，
∴a⊗(b×c) ≠ (a⊗b)×c. 否 (续表)
∵a⊗(b⊗c) = a⊗$\frac{bc}{b + c}$ = $\frac{abc}{a + \frac{bc}{b + c}}$ = $\frac{abc}{ab + ac + bc}$，(a⊗b)⊗c = $\frac{ab}{a + b}$⊗c = $\frac{abc}{ab + ac + bc}$，
∴a⊗(b⊗c) = (a⊗b)⊗c. 是
∵a⊗(b + c) = $\frac{a(b + c)}{a + b + c}$，a⊗b + a⊗c = $\frac{ab}{a + b}$ + $\frac{ac}{a + c}$，
∴a⊗(b + c) ≠ a⊗b + a⊗c. 否
∵a×(b⊗c) = a×$\frac{bc}{b + c}$ = $\frac{abc}{b + c}$，(a×b)⊗c = $\frac{abc}{ab + c}$，
∴a×(b⊗c) ≠ (a×b)⊗c. 否

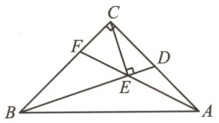
9. 如图,在$Rt\triangle ABC$中,$AC=BC=2$,$D$为边$AC$上的动点,过$C$作$CE\perp BD$于点$E$,连接$AE$并延长交$BC$于点$F$.当$AE$取得最小值时,则$AD$的长为 (C)


A.$\sqrt{5}-1$
B.$\frac{\sqrt{5}-1}{2}$
C.$3-\sqrt{5}$
D.$\frac{\sqrt{5}+1}{2}$

答案：
9 C 【解析】
∵CE ⊥ BD，
∴∠BEC = 90°，
∴点 E 在以 BC 为直径的圆上运动，如图，取 BC 的中点 O，以 O 为圆心，OB 的长为半径作⊙O，连接 OA 与⊙O 交于点 E'，连接 BE'并延长交 AC 于点 D'，由点到圆上的距离可知，当点 E 在 E'位置时，AE 取得最小值为 OA - OE'，在 Rt△ABC 中，AC = BC = 2，
∴OC = OE' = 1，OA = $\sqrt{OC² + AC²}$ = $\sqrt{5}$，
∴AE' = OA - OE' = $\sqrt{5}$ - 1，
∵OC = OE'，
∴∠OCE' = ∠OE'C，
∵∠BE'O + ∠CE'O = 90°，∠OCE' + ∠D'CE' = 90°，
∴∠D'CE' = ∠BE'O，
∵∠BE'O = ∠AE'D'，
∴∠D'CE' = ∠AE'D'，
∵∠CAE' = ∠E'AD'，
∴△CAE'∽△E'AD'，
∴$\frac{AC}{AE'}$ = $\frac{AE'}{AD'}$，
∵$\frac{2}{\sqrt{5} - 1}$ = $\frac{\sqrt{5} - 1}{AD'}$，
∴AD' = 3 - $\sqrt{5}$，即当 AE 取得最小值时，则 AD 的长为 3 - $\sqrt{5}$.故选 C.

10. 如图,在$Rt\triangle ABC$中,$AC=4$,$BC=3$,$\angle ACB$的平分线交斜边$AB$于点$D$,点$E,F$分别在边$CA,CB$上(不含端点),且$DE\perp DF$,设$AE=x$,$\triangle DEF$与$\triangle CEF$的面积之差为$y$,则$y$关于$x$的函数图象可能为 (A)

答案： 10 A 【解析】如图，过点 D 作 DH ⊥ BC，DG ⊥ AC，则 ∠DHF = ∠DGC = ∠DGE = 90°，
∵CD 为∠ACB 的平分线，
∴DH = DG，又
∵∠BCA = 90°，
∴四边形 CGDH 为正方形，
∴CH = CG = DG = DH，∠HDG = 90°，
∴tan B = $\frac{DH}{BH}$ = $\frac{AC}{BC}$ = $\frac{4}{3}$，
∴设 DH = 4a，BH = 3a，
∴CH = DH = 4a，
∴BC = BH + CH = 7a = 3，
∴a = $\frac{3}{7}$，
∴CH = CG = 4a = $\frac{12}{7}$，
∴AG = AC - CG = 4 - $\frac{12}{7}$ = $\frac{16}{7}$.①如图 1，当点 E 在 G 点右侧时，则 EG = AG - AE = $\frac{16}{7}$ - x，
∵DE ⊥ DF，∠HDG = 90°，
∴∠FDH = ∠EDG = 90° - ∠FDG，又
∵DH = DG，∠DHF = ∠DGE = 90°，
∴△DFH≌△DEG(AAS)，
∴DF = DE，HF = EG = $\frac{16}{7}$ - x，
∴CF = CH - HF = $\frac{12}{7}$ - $\frac{16}{7}$ + x = x - $\frac{4}{7}$，
∴S△CEF = $\frac{1}{2}$CE · CF = $\frac{1}{2}$(4 - x)(x - $\frac{4}{7}$)，在 Rt△DEG 中，由勾股定理得 DE² = DG² + EG² = ($\frac{12}{7}$)² + ($\frac{16}{7}$ - x)²，
∴S△DEF = $\frac{1}{2}$DE · DF = $\frac{1}{2}$DE² = $\frac{1}{2}$ × ($\frac{12}{7}$)² + $\frac{1}{2}$($\frac{16}{7}$ - x)²，
∴S△DEF - S△CEF = $\frac{1}{2}$ × ($\frac{12}{7}$)² + $\frac{1}{2}$($\frac{16}{7}$ - x)² - $\frac{1}{2}$(4 - x)(x - $\frac{4}{7}$)，整理，得 y = x² - $\frac{32x}{7}$ + $\frac{256}{49}$;②如图 2，当点 E 在点 G 左侧时，则 EG = AE - AG = x - $\frac{16}{7}$，CE = 4 - x，CF = CH + HF = $\frac{12}{7}$ + x - $\frac{16}{7}$ = x - $\frac{4}{7}$，DE² = ($\frac{12}{7}$)² + (x - $\frac{16}{7}$)²，
∴S△DEF - S△CEF = $\frac{1}{2}$ × ($\frac{12}{7}$)² + $\frac{1}{2}$(x - $\frac{16}{7}$)² - $\frac{1}{2}$(4 - x)(x - $\frac{4}{7}$)，整理，得 y = x² - $\frac{32x}{7}$ + $\frac{256}{49}$. 综上，y = x² - $\frac{32x}{7}$ + $\frac{256}{49}$ = (x - $\frac{16}{7}$)²(0 ＜ x ＜ 4)，
∴图象为顶点在 x 轴上的抛物线的一部分.故选 A.

11. $-8$的立方根是-2.

答案： 11 -2

12. 比较大小:$\sqrt{5}-2$＜$3-\sqrt{5}$(填“$\gt$”或“$\lt$”).

答案： 12 ＜

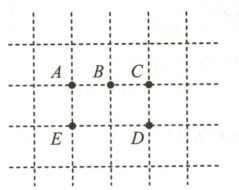
13. 如图,在一个正方形的网格上有$A,B,C,D,E$五个点,任意连接其中3个点,在构成的三角形中,是直角三角形的概率为$\frac{7}{9}$.

答案： 13 $\frac{7}{9}$ 【解析】从在格点上的点 A，B，C，D，E 中任取三个点构成的三角形有 △ABD，△ABE，△ACD，△ACE，△ADE，△BCD，△BCE，△BDE，△CDE，共 9 个，根据网格的特点可得△ACD，△BCD，△ADE，△ABE，△ACE，△BDE，△CDE 是直角三角形，即在构成的三角形中，是直角三角形的个数是 7，
∴在构成的三角形中，是直角三角形的概率为 $\frac{7}{9}$.

14. 为了适应新的考试评价改革,需要对学生的原始分进行转换,某班一次数学测试中,全班最高分是95分,最低分是45分.现将全班学生成绩作线性转换,原始分记为$x$,转换后的分数记为$y$,满足$y=a+bx$,其中$b\gt0$.转换后使得最高分为100分,最低分为30分.
(1)某同学原始分是80分,则转换后的分数是79.
(2)若全班原始分数的方差是225,则转换后的班级分数的方差是441.
方差参考公式:$S^{2}=\frac{(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+·s+(x_{n}-\overline{x})^{2}}{n}$.

答案： 14
(1)79(2分)
(2)441(3分) 【解析】
(1)由转换分规则，得$\begin{cases}a + 95b = 100 \\a + 45b = 30\end{cases}$，解得$\begin{cases}a = -33 \\b = 1.4\end{cases}$，
∴y = -33 + 1.4x，当 x = 80 时，y = 79.
(2)
∵y₁ = a + bx₁，y₂ = a + bx₂，y₃ = a + bx₃，⋯，yₙ = a + bxₙ，y = $\frac{1}{n}$(y₁ + y₂ + y₃ + ⋯ + yₙ) = a + bx. $S_y^2$ = $\frac{(y_1 - \bar{y})^2 + (y_2 - \bar{y})^2 + (y_3 - \bar{y})^2 + ⋯ + (y_n - \bar{y})^2}{n}$ = $\frac{(bx_1 - b\bar{x})^2 + (bx_2 - b\bar{x})^2 + (bx_3 - b\bar{x})^2 + ⋯ + (bx_n - b\bar{x})^2}{n}$ = $b^2\frac{(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + (x_3 - \bar{x})^2 + ⋯ + (x_n - \bar{x})^2}{n}$ = $b^2S_x^2$ = 441.