《2026年1号卷中考试题精编九年级数学安徽专版》

18. 新方向·项目式学习 数学兴趣小组开展了一项探究活动,主题是“两个相邻奇数/偶数的平方差”.相关内容如下表所示:

$16=5^{2}-3^{2}$
$24=7^{2}-5^{2}$
32$=$9² -7²
$\dots$|$4=2^{2}-0^{2}$
$12=4^{2}-2^{2}$
$20=6^{2}-4^{2}$
$28=8^{2}-6^{2}$
(1)完成上述表格内容.
(2)兴趣小组发现:4,8,12,16,$\dots$这些形如$4n$($n$是正整数)的数都可以用两个相邻奇数/偶数的平方差来表示,分析过程如下:
①设两个相邻奇数分别为:$2n+1$,$2n-1$($n$为正整数),
则:$(2n+1)^{2}-(2n-1)^{2}=8n=4× 2n$;
②设两个相邻偶数分别为:$2n$,$2n-2$($n$为正整数),
则:$(2n)^{2}-(2n-2)^{2}=8n-4=4(2n-1)$,
而$2n$,$2n-1$能取到所有的正整数,由此可证明结论正确.

答案： 18
(1)32;9²;7²;8n;(2n+1)²;(2n-1)²。 …(6分)
(2)(2n)²-(2n-2)²=8n-4=4(2n-1)。
………………(8分)

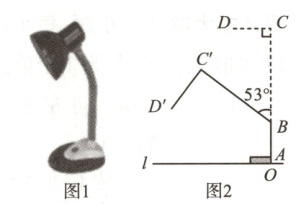
19. 如图1所示,在水平桌面上放置着一盏台灯.如图2,水平桌面记为$l$,台灯的底座OA高度为2 cm,支撑架AB长度为10 cm,连接杆BC长度为32 cm,且点A,B,C在一条直线上,灯盘CD与连接杆BC垂直,其长度为15 cm.如图2,当连接杆BC绕点B逆时针旋转$53^{\circ}$后得到$BC'$,且灯盘$C'D'$始终与连接杆$BC'$垂直,求此时点$D'$离桌面$l$的高度.(结果保留整数.参考数据:$\sin 53^{\circ}\approx \dfrac{4}{5}$,$\cos 53^{\circ}\approx \dfrac{3}{5}$,$\tan 53^{\circ}\approx \dfrac{4}{3}$)

答案： 19 解：如图，分别作C'E⊥BC于E，C'G⊥L于G，D'H⊥L于H，D'F⊥C'G于F，
∴BE=BC'cos53°≈32×$\frac{3}{5}=19.2$(cm)，
∠BC'F=∠C'BE=53°。 ………………(4分)
又
∵∠D'C'F+∠BC'F=90°，∠C'D'F+∠D'C'F=90°，
∴∠C'D'F=∠BC'F=53°，
∴C'F=C'D'sin53°≈15×$\frac{4}{5}=12$(cm)，
∴D'H=FG=C'G-C'F=EO-C'F=EB+BA+OA-C'F=19.2+10+2-12=19.2(cm)≈19(cm)。
答：此时点D'离桌面L的高度约为19cm …(10分)

20. 如图,在$\triangle ABC$中,以BC为直径的$\odot O$分别交AB,AC于点D,E,BE与CD交于点F,$\angle DFB=\angle ABC$.
(1)求证:$AC=BC$.
(2)若$BC=5$,$CE=3$,求AD的长.

答案： 20 解：
(1)证明：
∵∠DFB=∠ABC，
∴∠FBC+∠FCB=∠ABE+∠FBC，
∴∠ABE=∠FCB。
∵∠ABE=∠ACD，
∴∠ACD=∠BCD。
∵BC是直径，
∴∠BDC=∠ADC=90°，
∵∠A+∠ACD=90°，∠ABC+∠BCD=90°，
∴∠A=∠ABC，
∴AC=BC。 ………………(5分)
(2)
∵BC是直径，
∴∠BEC=∠AEB=90°，
∴BE=$\sqrt{BC²-CE²}=\sqrt{5²-3²}=4$，
∵CA=CB=5，CE=3，
∴AE=AC-CE=5-3=2，
∴AB=$\sqrt{AE²+BE²}=\sqrt{2²+4²}=2\sqrt{5}$，
∵CA=CB，CD⊥AB，
∴AD=DB=$\frac{1}{2}$AB=$\sqrt{5}$。 ………………(10分)
一题多解
(1)
∵BC是直径，
∴∠BDC=∠CEB=90°，
∴∠ADF=∠AEF=90°，
∴在四边形ADFE中，∠A+∠DFE=180°，
又
∵∠DFB+∠DFE=180°，
∴∠A=∠DFB。
∵∠DFB=∠ABC，
∴∠A=∠ABC，
∴AC=BC。