2026年1号卷中考试题精编九年级数学安徽专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年1号卷中考试题精编九年级数学安徽专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
8. 新课标·跨学科试题 生活中的很多变化都是物理变化或化学变化.下面的五张卡片除图片内容不同外,其他没有区别,放置于暗箱中摇匀.从中随机抽取两张卡片,卡片内容均为化学变化的概率为 (

A.$\frac{3}{5}$
B.$\frac{2}{5}$
C.$\frac{3}{10}$
D.$\frac{6}{25}$
C
)
A.$\frac{3}{5}$
B.$\frac{2}{5}$
C.$\frac{3}{10}$
D.$\frac{6}{25}$
答案:
8 C 【解析】将五张卡片分别记为A,B,C,D,E,其中卡片内容为化学变化的有A,D,E,
列表如下:
| | A | B | C | D | E |
| --- | --- | --- | --- | --- | --- |
| A | | (A,B) | (A,C) | (A,D) | (A,E) |
| B | (B,A) | | (B,C) | (B,D) | (B,E) |
| C | (C,A) | (C,B) | | (C,D) | (C,E) |
| D | (D,A) | (D,B) | (D,C) | | (D,E) |
| E | (E,A) | (E,B) | (E,C) | (E,D) | |
共有20种等可能的结果,其中卡片内容均为化学变化的结果有:(A,D),(A,E),(D,A),(D,E),(E,A),(E,D),共6种,
∴卡片内容均为化学变化的概率为$\frac{6}{20}$ = $\frac{3}{10}$.故选C.
列表如下:
| | A | B | C | D | E |
| --- | --- | --- | --- | --- | --- |
| A | | (A,B) | (A,C) | (A,D) | (A,E) |
| B | (B,A) | | (B,C) | (B,D) | (B,E) |
| C | (C,A) | (C,B) | | (C,D) | (C,E) |
| D | (D,A) | (D,B) | (D,C) | | (D,E) |
| E | (E,A) | (E,B) | (E,C) | (E,D) | |
共有20种等可能的结果,其中卡片内容均为化学变化的结果有:(A,D),(A,E),(D,A),(D,E),(E,A),(E,D),共6种,
∴卡片内容均为化学变化的概率为$\frac{6}{20}$ = $\frac{3}{10}$.故选C.
9. 新趋势·代数推理 已知$xy = x + y = k\neq0$,下列结论不正确的是 (
A.$\frac{1}{x}+\frac{1}{y}=1$
B.$(x - 1)^{2}+(y - 1)^{2}\geq2$
C.若$x,y$同号,则$k\geq4$
D.若$x,y$异号,则$-4\leq k\lt0$
D
)A.$\frac{1}{x}+\frac{1}{y}=1$
B.$(x - 1)^{2}+(y - 1)^{2}\geq2$
C.若$x,y$同号,则$k\geq4$
D.若$x,y$异号,则$-4\leq k\lt0$
答案:
9 D 【解析】逐项分析如下:
| 选项 | 分析 | 结论是否正确 |
| --- | --- | --- |
| A |
∵xy = x + y,
∴$\frac{xy}{xy}$ = $\frac{x + y}{xy}$,即1 = $\frac{1}{x}$ + $\frac{1}{y}$. | 是 |
| B |
∵(x - 1)² + (y - 1)² = x² - 2x + 1 + y² - 2y + 1 = x² + y² - 2(x + y) + 2 = (x - y)² + 2 ≥ 2. | 是 |
| C | 当x,y同号时,k = xy > 0,
∵xy = x + y = k,
∴y = $\frac{x}{x - 1}$,
∴xy = $\frac{x²}{x - 1}$ = k,即x² - kx + k = 0,由题意得,x² - kx + k = 0存在根,
∴Δ = k² - 4k ≥ 0,解得k ≤ 0或k ≥ 4,
∵k = xy > 0,
∴k ≥ 4. | 是 |
| D | 当x,y异号时,k = xy < 0,由选项C可知k² - 4k ≥ 0,解得k ≤ 0或k ≥ 4,
∵k = xy < 0,
∴k < 0,而不是 - 4 ≤ k < 0. | 否 |
故选D.
| 选项 | 分析 | 结论是否正确 |
| --- | --- | --- |
| A |
∵xy = x + y,
∴$\frac{xy}{xy}$ = $\frac{x + y}{xy}$,即1 = $\frac{1}{x}$ + $\frac{1}{y}$. | 是 |
| B |
∵(x - 1)² + (y - 1)² = x² - 2x + 1 + y² - 2y + 1 = x² + y² - 2(x + y) + 2 = (x - y)² + 2 ≥ 2. | 是 |
| C | 当x,y同号时,k = xy > 0,
∵xy = x + y = k,
∴y = $\frac{x}{x - 1}$,
∴xy = $\frac{x²}{x - 1}$ = k,即x² - kx + k = 0,由题意得,x² - kx + k = 0存在根,
∴Δ = k² - 4k ≥ 0,解得k ≤ 0或k ≥ 4,
∵k = xy > 0,
∴k ≥ 4. | 是 |
| D | 当x,y异号时,k = xy < 0,由选项C可知k² - 4k ≥ 0,解得k ≤ 0或k ≥ 4,
∵k = xy < 0,
∴k < 0,而不是 - 4 ≤ k < 0. | 否 |
故选D.
10. 如图,在$Rt\triangle ABC$中,$\angle ABC = 90^{\circ}$,$BC = 5$,$\tan\angle A=\frac{1}{2}$,点$D,E$分别在$AB,AC$边上,将$\triangle ADE$沿$DE$翻折得到$\triangle A'DE$,$A'E$与$AB$相交于点$F$,$A'D\perp AB$.若$\triangle BEF$与$\triangle BCE$面积相等,$AD$的长为 (

A.$3\sqrt{2}$
B.$\frac{10}{3}$
C.$\sqrt{5}+1$
D.$2\sqrt{3}$
B
)
A.$3\sqrt{2}$
B.$\frac{10}{3}$
C.$\sqrt{5}+1$
D.$2\sqrt{3}$
答案:
10 B 【解析】如图,作EH⊥AB于点H,
∵A'D⊥AB,可得∠A'DA = 90°,再由折叠性质可得∠ADE = ∠A'DE = $\frac{360° - 90°}{2}$ = 135°,AD = A'D,
∴∠EDH = 45°,从而△EDH为等腰直角三角形,
∴EH = DH,在Rt△ABC中,tan∠A = $\frac{1}{2}$,BC = 5,
∴AB = 10,同理可得AH = 2EH,故设AD = DH = EH = A'D = x,在△DFA'和△HFE中,$\begin{cases}∠A'DF = ∠EHF = 90°\\∠DFA' = ∠HFE\\A'D = EH\end{cases}$,
∴△DFA' ≌ △HFE(AAS),
∴DF = FH = $\frac{1}{2}$x,
∴BF = AB - AD - DF = 10 - $\frac{3}{2}$x,
∴S△BEF = $\frac{1}{2}$BF·EH = $\frac{1}{2}$x(10 - $\frac{3}{2}$x),S△BCE = $\frac{1}{2}$BC·BH = $\frac{5}{2}$·(10 - 2x),
∵△BEF与△BCE面积相等,
∴$\frac{1}{2}$x(10 - $\frac{3}{2}$x) = 25 - 5x,整理得3x² - 40x + 100 = 0,解得x = $\frac{10}{3}$或x = 10(舍去),即AD = $\frac{10}{3}$.故选B.
要点归纳:解决折叠问题的一般思考过程
图形折叠的本质是轴对称,解决折叠问题的关键是寻找图形中相等的线段、角。此类问题的一般思考过程如下:
(1)利用轴对称的性质找到折叠前后的不变量与变量。
(2)根据题目已知角、线段之间的关系,结合三角形的内角和定理、三角形的内角与外角的关系,把待求解的线段或角转移到相应的直角三角形、等腰三角形等特殊三角形中进一步求解。
(3)若简单的等量关系不能直接解决问题,则思考能否在构造出来的三角形中运用勾股定理、锐角三角函数、三角形的全等或相似等知识建立有关线段、角之间的联系。
(4)解答折叠问题中的计算问题,有时还需要将折叠图还原,而后利用折叠前后对应三角形、线段、角的关系以及相似三角形的性质、勾股定理等进行下一步的计算。
∵A'D⊥AB,可得∠A'DA = 90°,再由折叠性质可得∠ADE = ∠A'DE = $\frac{360° - 90°}{2}$ = 135°,AD = A'D,
∴∠EDH = 45°,从而△EDH为等腰直角三角形,
∴EH = DH,在Rt△ABC中,tan∠A = $\frac{1}{2}$,BC = 5,
∴AB = 10,同理可得AH = 2EH,故设AD = DH = EH = A'D = x,在△DFA'和△HFE中,$\begin{cases}∠A'DF = ∠EHF = 90°\\∠DFA' = ∠HFE\\A'D = EH\end{cases}$,
∴△DFA' ≌ △HFE(AAS),
∴DF = FH = $\frac{1}{2}$x,
∴BF = AB - AD - DF = 10 - $\frac{3}{2}$x,
∴S△BEF = $\frac{1}{2}$BF·EH = $\frac{1}{2}$x(10 - $\frac{3}{2}$x),S△BCE = $\frac{1}{2}$BC·BH = $\frac{5}{2}$·(10 - 2x),
∵△BEF与△BCE面积相等,
∴$\frac{1}{2}$x(10 - $\frac{3}{2}$x) = 25 - 5x,整理得3x² - 40x + 100 = 0,解得x = $\frac{10}{3}$或x = 10(舍去),即AD = $\frac{10}{3}$.故选B.
要点归纳:解决折叠问题的一般思考过程
图形折叠的本质是轴对称,解决折叠问题的关键是寻找图形中相等的线段、角。此类问题的一般思考过程如下:
(1)利用轴对称的性质找到折叠前后的不变量与变量。
(2)根据题目已知角、线段之间的关系,结合三角形的内角和定理、三角形的内角与外角的关系,把待求解的线段或角转移到相应的直角三角形、等腰三角形等特殊三角形中进一步求解。
(3)若简单的等量关系不能直接解决问题,则思考能否在构造出来的三角形中运用勾股定理、锐角三角函数、三角形的全等或相似等知识建立有关线段、角之间的联系。
(4)解答折叠问题中的计算问题,有时还需要将折叠图还原,而后利用折叠前后对应三角形、线段、角的关系以及相似三角形的性质、勾股定理等进行下一步的计算。
11. 计算:$\sqrt[3]{-8}+(-1)^{0}=$
-1
$$.
答案:
11 -1
12. 如图,两个三角板如图放置,其中$\angle BAC = \angle DAE = 90^{\circ}$,$\angle B = 30^{\circ}$,$\angle D = 45^{\circ}$,若$BC// DE$,则$\angle CAE$的度数为
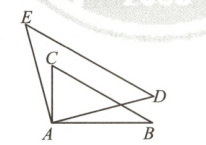
15°
.
答案:
12 15°
13. 如图,在$Rt\triangle OAB$中,$\angle ABO = 90^{\circ}$,反比例函数$y=\frac{k}{x}$的图象交$OA,AB$于点$C,D$,$\frac{OC}{OA}=\frac{2}{3}$,连接$CD$,若$\triangle ACD$的面积为$\frac{5}{4}$,则$k$的值是
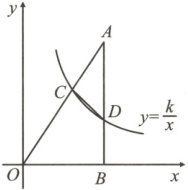
6
.
答案:
13 6 【解析】如图,过点C作CE⊥OB于点E,则CE//AB,
∴△OCE∽△OAB,
∴$\frac{OC}{OA}$ = $\frac{CE}{AB}$ = $\frac{OE}{OB}$ = $\frac{2}{3}$.设C(2m,$\frac{k}{2m}$),则OE = 2m,CE = $\frac{k}{2m}$,
∴OB = 3m,AB = $\frac{3k}{4m}$,则点D的坐标可设为(3m,$\frac{k}{3m}$),BE = m,
∴AD = $\frac{3k}{4m}$ - $\frac{k}{3m}$ = $\frac{5k}{12m}$,又
∵△ACD的面积为$\frac{5}{4}$,即$\frac{1}{2}$AD·BE = $\frac{5}{4}$,即$\frac{1}{2}$×$\frac{5k}{12m}$×m = $\frac{5}{4}$,解得k = 6.
y A
D y = $\frac{k}{x}$
0 EB x
∴△OCE∽△OAB,
∴$\frac{OC}{OA}$ = $\frac{CE}{AB}$ = $\frac{OE}{OB}$ = $\frac{2}{3}$.设C(2m,$\frac{k}{2m}$),则OE = 2m,CE = $\frac{k}{2m}$,
∴OB = 3m,AB = $\frac{3k}{4m}$,则点D的坐标可设为(3m,$\frac{k}{3m}$),BE = m,
∴AD = $\frac{3k}{4m}$ - $\frac{k}{3m}$ = $\frac{5k}{12m}$,又
∵△ACD的面积为$\frac{5}{4}$,即$\frac{1}{2}$AD·BE = $\frac{5}{4}$,即$\frac{1}{2}$×$\frac{5k}{12m}$×m = $\frac{5}{4}$,解得k = 6.
y A
D y = $\frac{k}{x}$
0 EB x
查看更多完整答案,请扫码查看


